Haptic Gaming System
Overview
Haptikos is an interactive gaming system that allows the user to physically feel a virtual world. The player controls the cursor on screen by moving the red joystick attached to the linkage system. Two games were created to highlight the capabilities of the feedback system. The first involves feeling a virtual shape displayed on the screen (the display can be toggled off if you want more of a challenge). This game is a simple demonstration of translating a virtual environment into something physical. The second is a side-scrolling level where the player collects jewels while avoiding boxes. This shows possible applications to an interactive gaming environment, where the user can directly feel what is happening to their character on screen.
The Team
- Yang Bai (Mechatronics Masters Student)
- Philip Dames (Mechanical Engineering MS/BS)
- Megan Welker(Mechanical Engineering BS/BM)
Mechanical Design
Existing System
Haptikos began as a modification of the pantograph used by John Glassmire for finger position tracking for his M.S. thesis work in friction-based tactile displays. This design allows the free point to move in a (roughly) semi-circular area in a plane. Two optical encoders are mounted at the shoulder joints to track the angle of the upper arm links (and thus the finger).
System Modifications
The existing system had the capability to accurately track finger position, but could not put apply any sort of haptic feedback. To add this capability, we chose to use a capstan drive system. In such a system, there is a thread spooled onto the motor shaft that winds in and out depending on how the motor is spinning. This thread is mounted to another element that is pulled back and forth as the thread spools out. Such drive systems can be found in other haptic devices (such as these haptic paddles) and are chosen because they increase the torque of a motor as a gearhead does, but avoid problems such as backlash which is a major concern when the goal is to provide smoothly changing forces to a user. The motors chosen for out project were the Pittman 700935 motors, which are relatively powerful motors without a gearhead.
The arc of the capstan drive was created by milling two 2.75" radius arcs out of Aluminum. A piece of heavy duty thread was set into the groove of the outer side of the arc and secured by screws on either side. To connect the capstan to the motor, the thread was tightly wound around the spool (3/8" diameter brass cylinder, mounted with a set screw) three times and pulled taut in the groove. The spool was covered with a plastic layer to increase the coefficient of friction between the spool and the thread. The gear ratio created by our drive system is 44 : 3 ().
Box
To enclose the entire system, we made a 12" x 12" x 3" acrylic box using the laser cutter. The top plate is removable so that the circuitry is readily accessible and holes were cut to create a mount for the pantograph and motors. A second bracket was also cut to hold the pantograph and motors in place, which was mounted inside the box, and holes were cut in the bottom of the box to allow the pantograph to be screwed into the base plate. Holes were cut in the side and back of the box to allow wires to pass in and out of the box.
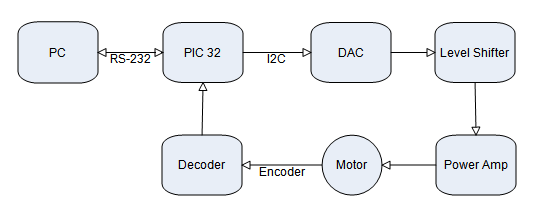
Electrical Design
PIC Configuration
We used the PIC32MX460F512L from Microchip on the NU32 board. The board was powered using a USB cable plugging into the socket on the left side of the board. The ribbon cable on the far right of the breadboard connects to the breakout board and has four I2C lines, four lines from the decoding circuit, +5V, and ground. The cable next to it is the RS-232 that connects the PIC to the PC.
Breakout Board
This board serves as a central hub for all of the other components to the circuit, allowing for only one ribbon cable to connect to the PIC's breadboard. Clockwise from the green power supply board, we have connections to the two power amplification circuits, the PIC breadboard, the decoding circuit, and the DAC/level shifting circuit. The power supply provides a separate +5V, -5V, and ground line to power the motors, protecting the PIC from the high amperage needed to drive the motors. In the center of the board is a Cincon EC2A05 DC/DC converter that takes in the +/- 5V lines and outputs +/- 15V used for the level shifting circuit.
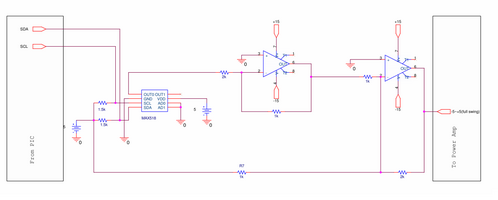
DAC/Level Shifter Board
This board takes the force data sent over I2C from the PIC (from the PC) and creates an analog voltage signal ranging from +/- 5V that feeds into the power amplification circuit. Here, we use a MAX518 DAC chip that connects to a level shifting circuit using 2 LT1001 op-amps, as shown in the circuit diagram. This is necessary to allow the motors to spin in both directions without the use of PWM (which we opted not to use because we want torque, and thus, current control). Note the actual board consists of two identical channels, one for each motor, while the schematic shows only one.
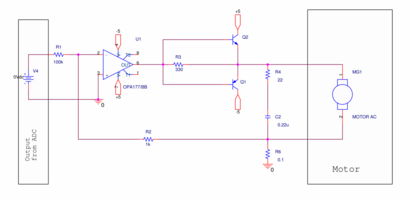
Motor Control Board
This circuit uses current feedback in order to maintain a constant output current, allowing for direct torque control of the motors. This circuit was designed by Prof. Peshkin and detailed information can be found here. Two of these boards were used, one for each motor with the input coming from the DAC board and power from the central breakout board.
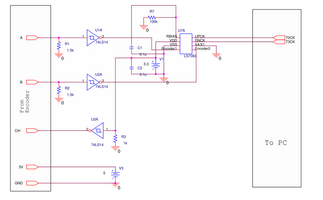
Decoder Board
The decoding circuit reads the signals from two optical encoders them into up and down counts (two each) that connect to the timer pins on the PIC. The encoders used are Canon TR-1 (equivalent to TR-36) which are 3600 counts per revolution using x1 decoding. The decoding circuit is that used in the Recommended Receiving Circuit link at the bottom of the page, where the channels first feed into a SN74HC14N Schmitt trigger which cleans up the signals going into the LS7083 quadrature decoding chips. These take the pulse trains and translate them into up and down counts which are then sent over to the PIC.
Mathematical Analysis of the Pantograph
There are two parts to this problem, the forward kinematics and the force generation, which are duals of each other.
Forward Kinematics
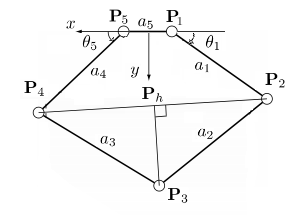
The forward kinematics of a system (typically a robotic arm or something similar) is often used in robotics and gaming to calculate the position and orientation of a hand given the joint angles of an arm. The idea is to create a function such that where is a vector giving the location of the finger and is a vector of the joint angles (here the angles read by the encoders). For our system, the pantograph used was originally designed and build by John Glassmire (formerly of the Laboratory of Intelligent Mechanical Systems. Dimensions as well as full calculations of the forward kinematics may be found in Appendix D and Solidworks drawings of the parts found in Appendix E of the paper found at [1]. Encoder 1 is found at angle 1, encoder 2 at angle 5, and the finger at angle 3, with arrows indicating the direction of positive motion, note that angle 5 is backwards to provide reflectional symmetry about the vertical axis.
Force Generation
Obviously, the wider the range of forces we can create, both in terms of magnitude and direction, the better sensation we are able to create with Haptikos. However, we also want to transition between forces in such a way that feels natural to the user. These are fundamental issue addressed by designers for any haptic device. There is a limit to the torques our motors can provide (current supply to each motor is limited to 500 mA), and thus on the strength of the forces we can give to the user and the resolution of these forces was also limited by communication issues (as discussed later).
We independently confirmed the forward kinematic calculations, and through a series of substitutions, put them all into a single function . Taking the derivative of this mapping, we have that , where is the Jacobian of the map. By the duality of velocity and force, we have that the torques required to produce a given force can be found using the relation . For our map, the Jacobian is complicated and would take up nearly a page so it is omitted for brevity. However, we were unsuccessful using this approach to generate forces in arbitrary directions. This may be due to many causes, from data types conflicting to omitting a sign or term when typing out the equations.
Instead we used simple controls to achieve forcing in eight directions. A single byte of data was sent to the PIC containing the motor control information, with the first nibble to control motor 1 and the second to control motor 2. This allows for 16 levels of forcing, with 7 chosen to indicate zero force. Less than 7 provided a torque along the positive direction for each angle (as indicated in the figure) and greater than 7 along the negative direction. We found that activating both motors allowed us to create forces along the y and x axis (depending on if the motors were providing a torque in the same, or opposite, directions, respectively) while only activating a single motor provided forcing along the lines y = x and y = -x (motor 2 or motor 1, respectively). This range of 16 discrete force values was mapped over half of the possible force range because we found that having forces that were too strong caused for large jumps when the forces changed direction while smaller forces allowed for smoother-feeling transitions, at the cost of a more rigid feeling to surfaces.
Software
PIC Programing
All PIC programming was done in C using the MPLAB IDE by Microchip Technologies. To install MPLAB, follow the instructions found here. To create a new project in MPLAB, follow the instructions found here. The source files for our project can be downloaded here (remember to change the include directions if you are trying to use our MPLAB project files).
While the source code is commented, here is a list of the project-specific files and a brief summary of the contents of each.
- fingerTrack.c - This is the main file of the project, containing the main function as well as initialization and communication functions
- initEncoder - This initializes the 4 timers (T2CK - T5CK) used to count the up and down pulses from the decoding circuit. Timers 2 and 3 are for the up and down counts of encoder 1, respectively. Timers 4 and 5 are used for up and down counts of encoder 2.
- getEncoderPositionX - This reads the current counts of encoder X and updates the angles, checking for rollover of the 16-bit counters.
- initUART1 - This initializes the UART1 bus of the PIC to be used for RS-232 communication with the PC.
- initInterruptComm - This initializes the Timer1 interrupt to run every 10ms and initializes both I2C buses on the PIC to talk to the DAC's. The interrupt timing could be synched to match the frame rate of the game, but we found this to be reliable and not interfere with the data transmission interrupt.
- MAX518 - This takes the data sent from the PC about how to force the system, parses the data, and sends out the appropriate signal to the DAC's over the I2C buses. Only 1 byte of data is sent between the PC and the PIC as this was found to be the most reliable, though it does limit the resolution of forces we are able to achieve (16 levels instead of 256). We did not find this to be a problem, but is one area of possible improvement.
- UART1 interrupt - When it detects that it has received data from the PC, the PIC will read the data, call the MAX518 function, and toggle LED0 for visual feedback. We had some issues with the interrupt not functioning correctly after the game was reset after a game over (this did not happen every time).
- Timer1 interrupt - This sends the current (x,y) position of the finger as well as the two angles of the encoders to the PC.
- calculations.c (and .h) - This library has the functions used to calculate the forward kinematics of the pantograph (i.e., to get finger position from the encoder readings).
- sine and cosine - These functions take in the current encoder angle (measured to the nearest tenth of a degree) as an integer and use a lookup table to calculate the sine. The output is an integer which must be divided by 10000 (the global variable SCALER). This was done to speed up calculations as it only involves integer math instead of floats, and can directly use encoder counts instead of converting these to radians.
- forwardKinematics - This calculates the current (x,y) location of the finger based on the current encoder readings.
Game Programming
The games are programmed and run in the Processing language (find out more information here). We chose to make two games that highlight different aspects of our project, though as you can imagine, our system could be used for many more.
Link's Adventure
This game is a side-scrolling adventure game where the player must avoid the blocks and collect the jewels scrolling across the screen. As the player icon, we chose to use the character Link from the original Legend of Zelda game due to the simple graphics and game style. The three types of jewels each have a different effect on the game. Red replenish health lost from hitting the boxes, green increase the score, and blue slow blocks (whose speed gradually increases over time). When Link runs into a red block, Haptikos will shake the joystick as the box disappears to give the user a physical indication that their player was injured, much like the rumble feature found in many modern game console controllers. While the user has the option of going for a high score, we have found that it is generally more enjoyable to simply run into the blocks as this is the unique part of our device. Future iterations of this game would include some sort of haptic feedback when a jewel is collected to the player strikes the ground, possibly even simulating gravity by pushing the character towards the ground. Commented source code can be found here and code allowing the game to be played with a computer mouse here.
Identification Game
In this game the player will feel a virtual shape (circle, star, triangle, square, or diamond) in the center of the screen. When the cursor (blue circle) hits the shape, the device will push the finger away from the shape, creating the sensation that you are feeling a wall. The player can also play blindly, using only the feedback from Haptikos to attempt to identify the invisible shape. To toggle this mode, press the 'i' key on the keyboard. Press 'r' to generate a new shape at random. Currently there are only 5 shapes, chosen because they are different enough so that the user can identify the shape (i.e., a heptagon and an octagon would be too similar to identify using the discrete forces available to us). Commented source code can be found here.