Rotational Stiffness

Stiffness

Stiffness (k) is the relationship between an applied force and the displacement the force produces. This relationship can be defined for two common cases:

In the linear case, the applied force (F) is proportional to the linear displacement (x) of one end of the "spring" with respect to the other (i.e. the amount of stretch or compression of the spring).

F = k * x

In the rotational case, the applied torque (T) is proportional to the angular displacement (theta) of one side/end with respect to the other.

T = k * theta

In both cases, the relationship can be non-linear, however a linear relationship is easier to work with.

Linear Spring

Extension springs avaiable through Ganga Spring Industries

A linear extension spring is generally a coil, usually made of a tempered steel. The thickness of the wire used to make the spring and the number and diameter of the coils determines the stiffness. Over the elastic extension range for the spring, the relationship between the extension of the spring and the force required to attain that extension is linear. This type of spring obeys Hook's Law:

F = k * x

Torque/Moment

For a constant torque, as the distance from the axis doubles, the force needed is halved

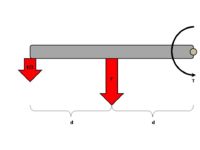
A torque (T), or moment, is the product of the force (F) applied tangentially to the rotation of an object (i.e. perpendicular to the axis ALONG the rotating member) and the distance (d) between the axis of rotation and the location of the applied force. In short, this amounts to the effect of a lever. A longer "arm" increases the torque provided by a given force. In converse, for a constant torque, the force produced is inversely related to the distance, so at twice the distance the force is halved. This is shown in the figure at right, and the relationship is given by the formula:

T = F * d

Vector Decomposition

Vector decomposition diagram

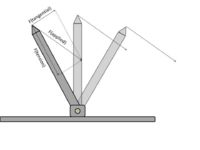
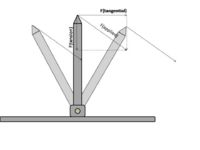
The sum of two vectors can be described by a single vector (the resultant). At right is a figure which shows how two vectors can be summed to produce a resultant, and how a single vector can be reduced to two orthogonal components.

Vector decomposition for a constant force at one of three angles

Applying this vector decomposition to the forces applied to a rotating member, it is possible to decompose an applied force to two components:

The axial component is the force directed along the long axis of the rotating member. This force is a compressive force.

The tangential component is the force directed perpendicular to the long axis of the rotating member. This force produces a torque or moment about the axis of rotation.

Vector decomposition for a constant force at the second of three angles

Vector decomposition for a constant force at the third of three angles