Difference between revisions of "Capstone Dev"
| Line 243: | Line 243: | ||
# '''Your commented code in a directory called "code."''' Your code should be lightly commented, so it is clear to the reader what the code is doing. No need to go overboard, but keep in mind your reviewer may not be fluent in your programming language. Your code comments must include an example of how to use the code. Only turn in functions that you wrote or modified; you don't need to turn in other MR functions that your code uses. If your code is in MATLAB or Python, just turn in the text files with your functions. If your code is in Mathematica, turn in (a) your .nb notebook file and (b) a .pdf printout of your code, so a reviewer can read your code without having to have the Mathematica software. Ideally your code would automatically generate a .csv file, but it is also acceptable if it simply prints out the comma-separated values, which then must be copy-and-pasted into a text editor to create the .csv file. |
# '''Your commented code in a directory called "code."''' Your code should be lightly commented, so it is clear to the reader what the code is doing. No need to go overboard, but keep in mind your reviewer may not be fluent in your programming language. Your code comments must include an example of how to use the code. Only turn in functions that you wrote or modified; you don't need to turn in other MR functions that your code uses. If your code is in MATLAB or Python, just turn in the text files with your functions. If your code is in Mathematica, turn in (a) your .nb notebook file and (b) a .pdf printout of your code, so a reviewer can read your code without having to have the Mathematica software. Ideally your code would automatically generate a .csv file, but it is also acceptable if it simply prints out the comma-separated values, which then must be copy-and-pasted into a text editor to create the .csv file. |
||
# '''A directory called "results" with the results of your program.''' This directory should contain two directories: one titled "best" and one titled "overshoot." The directory "best" should contain the results using a well-tuned controller, either feedforward-plus-P or feedforward-plus-PI. The convergence exhibited by the controller does not necessarily have to be fast, but the motion should be smooth, with no overshoot, and very little error by partway through trajectory segment 1. The directory "overshoot" should contain the results using a less-well-tuned controller, one that exhibits overshoot and a bit of oscillation. Nonetheless, the error should be eliminated before the end of trajectory segment 1. Your controller for these results will likely be feedforward-plus-PI or just PI. In each of the two directories, give: |
# '''A directory called "results" with the results of your program.''' This directory should contain two directories: one titled "best" and one titled "overshoot." The directory "best" should contain the results using a well-tuned controller, either feedforward-plus-P or feedforward-plus-PI. The convergence exhibited by the controller does not necessarily have to be fast, but the motion should be smooth, with no overshoot, and very little error by partway through trajectory segment 1. The directory "overshoot" should contain the results using a less-well-tuned controller, one that exhibits overshoot and a bit of oscillation. Nonetheless, the error should be eliminated before the end of trajectory segment 1. Your controller for these results will likely be feedforward-plus-PI or just PI. In each of the two directories, give: |
||
## A very brief README.txt or README.pdf file that indicates the controller used or any other information about the results. |
|||
## A log file showing the program being called with the input. |
|||
## The V-REP .csv file produced by the program. |
|||
## The animation (a video) of your .csv file being animated by the V-REP scene. |
|||
## The <math>X_{\text{err}}</math> data file produced by your program. |
|||
## A plot of the six elements of <math>X_{\text{err}}</math> as a function of time, showing the convergence to zero. |
|||
'''Project grading.''' Your project will be graded on the clarity and correctness of your README files and your code. Your "results" directories will be graded on their correctness, including whether your error plots show reasonable convergence to zero and the quality of your videos. |
'''Project grading.''' Your project will be graded on the clarity and correctness of your README files and your code. Your "results" directories will be graded on their correctness, including whether your error plots show reasonable convergence to zero and the quality of your videos. |
||
Revision as of 12:42, 31 May 2018
This page describes the Capstone Project for the Coursera "Modern Robotics" Specialization. This project forms the sixth and final course of the Specialization: "Modern Robotics, Course 6: Capstone Project, Mobile Manipulation." This project draws on pieces of Courses 1 to 5.
A video summary of this project is given in this YouTube video.
Depending on your experience with programming, this project should take approximately 20 hours, broken down into three intermediate milestones and your final submission.
You should use the Modern Robotics code library to help you complete this project.
Introduction
In your capstone project, you will write software that plans a trajectory for the youBot mobile manipulator (a mobile base with four mecanum wheels and a 5R robot arm), performs odometry as the chassis moves, and performs feedback control as the youBot picks up a block at a specified location, carries it to a desired location, and puts it down.
The final output of your software will be a comma separated values (csv) text file that specifies the configurations of the chassis and the arm, the angles of the four wheels, and the state of the gripper (open or closed) as a function of time. This specification of the position-controlled youBot will then be "played" on the V-REP simulator to see if your trajectory succeeds in solving the task.
This project uses the CSV Mobile Manipulation youBot scene. You should download it and test it with the sample csv file, to see what a solution looks like.
Unlike previous projects, where we used V-REP to simply visualize the robot's motion, in this project V-REP will use a physics simulator to simulate the interaction of the youBot with the block. In other words, if the gripper closes on the block in the wrong position or orientation, the block may simply slide out of the grasp.
The V-REP scene drives the chassis configuration according to the sequence of chassis configurations in your csv file. For the robot arm, simulated high-gain controllers at the arm joints cause the arm to closely follow the configurations in your csv file.
The interaction between the robot and the block is governed by a physics simulator, often called a "physics engine," which approximately accounts for friction, mass, inertial, and other properties. V-REP has different physics engines which you can select, including Bullet and ODE.
The time between each successive configuration in your csv file is 0.01 seconds (10 milliseconds). A typical line of your csv file would be something like
-0.75959, -0.47352, 0.058167, 0.80405, -0.91639, -0.011436, 0.054333, 0.00535, 1.506, -1.3338, 1.5582, 1.6136, 0
i.e., thirteen values separated by commas, representing
chassis phi, chassis x, chassis y, J1, J2, J3, J4, J5, W1, W2, W3, W4, gripper state
where J1 to J5 are the arm joint angles and W1 to W4 are the four wheel angles.
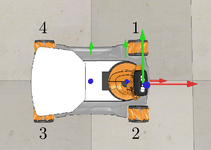
Wheels 1 to 4 are numbered as shown in the image to the right. The ten angles (phi for the chassis, five arm joint angles, and four wheel angles) are in radians and the two chassis position coordinates (x,y) are in meters. A gripper state of 0 indicates that you want the gripper to be open, and a gripper state of 1 indicates that you want the gripper to be closed. In practice, the transition from open to closed (or from closed to open) takes up to one second, so any transition from 0 to 1, or 1 to 0, in your csv file will take some time to complete.
Your program will take as input:
- the initial resting configuration of the cube object (which has a known geometry), represented by a frame attached to the center of the object
- the desired final resting configuration of the cube object
- the actual initial configuration of the youBot
- the reference initial configuration of the youBot (which will generally be different from the actual initial configuration, to allow you to test feedback control)
- optionally: gains for your feedback controller (or these gains can be hard-coded in your program)
The output of your program will be:
- a single csv file which, when "played" through the V-REP scene, should drive the youBot successfully pick up the block and put it down at the desired location
- a data file containing the 6-vector error as a function of time in tracking the reference trajectory of the end-effector
Your solution must employ automated planning and control techniques from this Coursera specialization. It should not simply be a manually coded trajectory of the robot. Your solution should automatically go from the input to the output, with no other human intervention. In other words, it should automatically produce a working csv file even if the input conditions are changed.
In your software, you should first piece together a reference trajectory for the gripper of the robot, which the robot is then controlled to follow. A typical reference trajectory would consist of the following segments:
- A trajectory to move the gripper from its initial configuration to a "standoff" configuration a few cm above the block.
- A trajectory to move the gripper down to the grasp position.
- Closing of the gripper.
- A trajectory to move the gripper back up to the "standoff" configuration.
- A trajectory to move the gripper to a "standoff" configuration above the final configuration.
- A trajectory to move the gripper to the final configuration of the object.
- Opening of the gripper.
- A trajectory to move the gripper back to the "standoff" configuration.
Segments 3 and 7 each keep the end-effector fixed in space but, at the beginning of the segment, change the state of the gripper from 0 to 1 or 1 to 0, waiting one second for the gripper closing to complete. In other words, each of these segments would consist of 100 identical lines of the csv file (corresponding to one second), where the first line has a gripper state different from the previous line in the csv file, to initiate the opening or closing.
Segments 2, 4, 6, and 8 are simple up or down translations of the gripper of a fixed distance. Good trajectory segments would be cubic or quintic polynomials taking a reasonable amount of time (e.g., one second).
Trajectory segments 1 and 5 are longer motions requiring motion of the chassis. Segment 1 is calculated from the desired initial configuration of the gripper to the standoff configuration, and segment 5 is calculated from the first standoff configuration to the second standoff configuration. The gripper trajectories could correspond to constant screw motion paths or decoupled Cartesian straight-line motion plus rotational motion, time scaled by third-order polynomials (Chapter 9).
Once the entire gripper reference trajectory has been pieced together from the 8 segments, the actual trajectory of the youBot is obtained by using a Jacobian pseudoinverse position controller as described in Chapter 13.5. Starting from the actual initial robot configuration (which has some error from the beginning of reference segment 1), your controller drives the gripper to follow segment 1, so that the gripper is at the standoff configuration for the beginning of segment 2. Your feedback controller should eliminate initial error before the gripper attempts to grasp the block, to avoid failure.
You are welcome to adopt a different approach to solving the pick-and-place problem, provided your approach takes the same inputs specified above, produces a csv file that successfully achieves the task, and is fully automatic (i.e., it works for different initial and final configurations of the block, different initial and reference configurations for the youBot, and requires no human intervention).
To simulate the effect of feedback control, you must write your own motion simulator. For each timestep, you take the initial configuration of the robot and the wheel and joint speeds calculated by your controller and numerically integrate the effect of these speeds over a timestep to get the new robot configuration. To calculate the new configuration of the chassis due to the wheel motions, you must implement an odometry step (Chapter 13.4).
Kinematics of the youBot
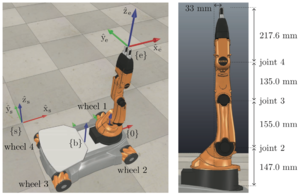
The images to the right illustrate the youBot. Click on them to make them bigger. The description below is consistent with Exercise 13.33 from the book, if you prefer to see the information there. All distances are in meters and all angles are in radians.
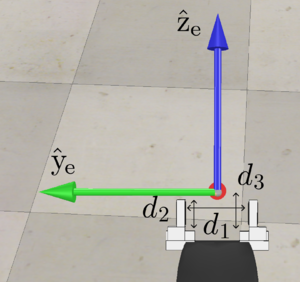
The configuration of the frame {b} of the mobile base, relative to the frame {s} on the floor, is described by the 3-vector or the matrix
where meters is the height of the {b} frame above the floor. The forward-backward distance between the wheels is meters and the side-to-side distance between wheels is meters. The radius of each wheel is meters. The forward driving and "free sliding" direction of each wheel is indicated in the figures.
The fixed offset from the chassis frame {b} to the base frame of the arm {0} is
When the arm is at its home configuration (all joint angles zero, as shown in the figure), the end-effector frame {e} relative to the arm base frame {0} is
When the arm is at its home configuration, the screw axes for the five joints are expressed in the end-effector frame {e} as
In this project, for simplicity we assume no joint limits on the five joints of the robot arm. It is recommended, however, that you choose limits on the wheel and joint velocities. We will come back to this issue later.
The end-effector frame {e} is rigidly attached to the last link and is midway between the tips of the gripper fingers. The minimum opening distance of the gripper is cm, the maximum opening distance is cm, the interior length of the fingers is cm, and the distance from the base of the fingers to the frame {e} is cm. When the gripper closes, it closes until it reaches its minimum closing distance or encounters a force large enough to prevent further closing.
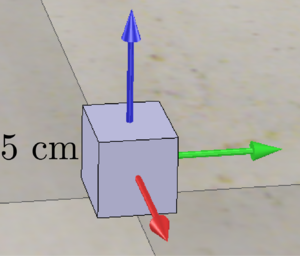
The object being manipulated is a cube, 5 cm x 5 cm x 5 cm. The cube's frame {c} is at the center of the cube, and the axes are aligned with the edges of the cube. The initial configuration of the cube is at (x, y, z) = (1, 0, 0.025 ) m in the space frame {s}, and the axes of {c} are aligned with {s}. The desired final configuration of the cube is at (x, y, z) = (0, 1, 0.025) m and the axes of {c} are rotated by about the axis of {s}. A good choice for the "standoff" configuration before moving down to the cube and moving back up (the ends of trajectories 1, 4, 5, and 8) is to have the {e} frame a few cm above the {c} frame.
What You Will Do
Your solution to this project will be a fairly complex piece of software. To help you structure the project, and to allow you to test individual pieces of your solution, the project has three milestones before you finally complete the project. You do not turn in your solutions to these milestone subprojects; you only turn in your final project.
Milestone 1: youBot Kinematics Simulator and csv Output
You will write a simulator for the kinematics of the youBot. The main function in the simulator, let's call it NextState, is specified by the following inputs and outputs:
Input:
- A 12-vector representing the current configuration of the robot (3 variables for the chassis configuration, 5 variables for the arm configuration, and 4 variables for the wheel angles).
- A 9-vector of controls indicating the arm joint speeds (5 variables) and the wheel speeds (4 variables).
- A timestep .
- A positive real value indicating the maximum angular speed of the arm joints and the wheels. For example, if this value is 12.3, the angular speed of the wheels and arm joints is limited to the range [-12.3 radians/s, 12.3 radians/s]. Any speed in the 9-vector of controls that is outside this range will be set to the nearest boundary of the range. If you don't want speed limits, just use a very large number. If you prefer, your function can accept separate speed limits for the wheels and arm joints.
Output:
- A 12-vector representing the configuration of the robot time later.
The function NextState is based on a simple first-order Euler step, i.e.,
- new arm joint angles = (old arm joint angles) + (joint speeds) *
- new wheel angles = (old wheel angles) + (wheel speeds) *
- new chassis configuration is obtained from odometry, as described in Chapter 13.4
To test your NextState function, you should put it inside a loop that simulates constant controls for one second. For example, you can set to 0.01 seconds and run a loop that calls NextState 100 times with the constant controls . Your program should write a csv file, where each line has 13 values separated by commas (the 12-vector consisting of 3 chassis configuration variables, the 5 arm joint angles, and the 4 wheel angles, plus a "0" for "gripper open") representing the robot's configuration after each integration step. Then you should load the csv file into the CSV Mobile Manipulation youBot V-REP scene and watch the animation of the constant controls to see if your NextState function is working properly (and to check your ability to produce a csv file).
Sample controls to try: Simulate the following controls for 1 second and watch the results in the V-REP scene.
- . The robot chassis should drive forward (in the direction by 0.475 meters.
- . The robot chassis should slide in the direction by 0.475 meters.
- . The robot chassis should spin counterclockwise in place by radians.
If the chassis motion is not what is described, then something is wrong with your implementation of odometry. You should also check that your wheel angles and arm joint angles are being updated properly, but this should be easy.
You should also try specifying a speed limit of 5 for the joints and wheels, then try the same tests above. Since your commanded controls exceed the speed limit, your function should properly restrict the actual speeds executed by the wheels and joints to the range [-5, 5]. As a result, the chassis should only move half the distance in these tests.
Milestone 2: Reference Trajectory Generation
For this milestone you will write a function TrajectoryGenerator to generate the reference trajectory for the end-effector frame {e}. This trajectory consists of eight concatenated trajectory segments, as described above.
Input:
- The end-effector's initial configuration: .
- The cube's initial configuration: .
- The cube's desired final configuration: .
- The standoff configuration above the cube, before and after grasping, relative to the cube: . This specifies the configuration of the end-effector {e} relative to the cube frame {c} before lowering to grasp, for example. If you would like to specify the standoff configuration in a different way, you are welcome to.
- The number of trajectory reference points per 0.01 seconds: . The value is an integer with a value of 1 or greater. Although your final animation will be based on snapshots separated by 0.01 seconds in time, the points of your reference trajectory (and your controller servo cycle) can be at a higher frequency. It is fine to choose if you'd like to keep things simple.
Output:
- An matrix. is the number of reference points in the entire concatenated eight-segment reference trajectory. Each of the rows represents a configuration of the end-effector frame {e} relative to {s} at that instant in time. Twelve of the 13 entries of a matrix row are the top three rows of the transformation matrix at that instant of time, i.e., from
and the 13th entry is the gripper state: 0 = open, 1 = closed. Keep in mind that opening and closing the gripper takes up to 1 second (initiated when the gripper state transitions from 0 to 1, or 1 to 0), so the trajectories involving opening and closing the gripper should keep the {e} frame stationary while the gripper completes its motion.
- A csv file with the entire eight-segment reference trajectory. Each line of the csv file corresponds to one configuration of the end-effector, expressed as 13 variables separated by commas. The 13 variables are, in order,
r11, r12, r13, r21, r22, r23, r31, r32, r33, px, py, pz, gripper state
It is up to you to determine the duration of each trajectory segment, but it is recommended that each segment's duration be an integer multiple of 0.01 seconds. You could automatically choose the duration of each trajectory segment to be equal to the maximum of: the distance the origin of the {e} frame has to travel divided by some reasonable maximum linear velocity of the end-effector, and the angle the origin of the {e} frame has to travel divided by some reasonable maximum angular velocity of the end-effector. The duration of each trajectory should not be so short as to require unreasonable joint and wheel speeds.
Your TrajectoryGenerator function is likely to use either ScrewTrajectory or CartesianTrajectory, from the Modern Robotics code library, to generate the individual segments.
Testing your function: We have created a V-REP scene to help you test your TrajectoryGenerator function. This scene reads in your csv file and animates it, showing how the end-effector frame moves as a function of time. You should verify that your TrajectoryGenerator works as you expect before moving on with the project.
Milestone 3: Feedforward Control
Now that you are able to simulate the motion of the robot and generate a reference trajectory for the end-effector, you are ready to begin experimenting with feedback control of the mobile manipulator. You will write the function FeedbackControl to calculate the kinematic task-space feedforward plus feedback control law, written both as Equation (11.16) and (13.37) in the textbook:
Input:
- The current end-effector reference configuration .
- The end-effector reference configuration at the next timestep in the reference trajectory, .
- The current actual end-effector configuration (also written ).
- The PI gain matrices and .
- The timestep between reference trajectory configurations.
Output:
- The commanded end-effector twist expressed in the end-effector frame {e}.
To calculate the control law FeedbackControl, we need the current actual end-effector configuration , a function of the chassis configuration and the arm configuration . The values come directly from the simulation results (Milestone 1). In other words, assume perfect sensors and odometry.
The error twist that takes to in unit time is derived from . FeedbackControl also needs to maintain an estimate of the integral of the error, e.g., by adding to the running total at each timestep. The feedforward reference twist that takes to in time is derived from .
The output of FeedbackControl is the commanded end-effector twist expressed in the end-effector frame {e}. To turn this into commanded wheel and arm joint speeds , we use the pseudoinverse of the mobile manipulator Jacobian ,
Now write your full program, according to the input specifications at the top of this page. Your program should first generate a reference trajectory using TrajectoryGenerator and set the initial robot configuration, a 13-vector as described earlier on this page:
chassis phi, chassis x, chassis y, J1, J2, J3, J4, J5, W1, W2, W3, W4, gripper state
Now you enter a loop that loops through the reference trajectory generated by TrajectoryGenerator. If the reference trajectory has reference configurations, the loop runs times. For example, the 10th time through the loop, the controller uses the 10th configuration of the reference trajectory as and the 11th configuration to help calculate the feedforward twist .
Each time through the loop, you calculate the control law using FeedbackControl and generate the wheel and joint controls using ; send the controls, configuration, and timestep to NextState to calculate the new configuration; and store every th configuration for later animation. (Note that the reference trajectory has reference configurations per 0.01 second step, as described in Milestone 2. You may choose for simplicity.) You should also store every th 6-vector, so you can later plot the evolution of the error over time.
Once the loop has completed, write out the csv file of configurations. If the total time of motion of the youBot is 15 seconds, your csv file should have 1500 lines (or 1501 lines), corresponding to 0.01 seconds between each configuration. Load the csv file into the CSV Mobile Manipulation youBot scene to see the results. Your program should also generate a file with the log of the 6-vector as a function of time, suitable for plotting by your favorite plotting software.
Testing feedforward control: You should make sure feedforward control works as you expect before testing feedback control. Choose an initial configuration of the robot that puts the end-effector exactly at the configuration of the beginning of the reference trajectory. Run your program with , i.e., feedforward control only. This should result in a csv file which, when played through the V-REP scene, drives the robot to pick up the block and put it down at the desired configuration. If not, time to start debugging! Your end-effector reference trajectory must be correct, if you already tested Milestone 2. So now you have to figure out why the wheel and arm controls your feedforward controller and Jacobian pseudoinverse are generating do not drive the end-effector along the reference trajectory.
You should also try starting the end-effector with some initial error from the reference trajectory. See how the end-effector moves under these circumstances. Does it make sense to you?
Do not move on with the project until your feedforward control works as you expect. Otherwise the effects of PI feedback control will only further confuse the situation.
Completing the Project and Your Submission
Now that feedforward control is working, you are ready to complete your project. Let the initial configuration of the end-effector reference trajectory be at
Choose an initial configuration of the youBot so that the end-effector has at least 30 degrees of orientation error and 0.2 m of position error. Try executing the feedforward controller () to see what happens.
Now add a positive-definite diagonal proportional gain matrix while keeping the integral gains zero. You can keep the gains "small" initially so the behavior is not much different from the case of feedforward control only. As you increase the gains, can you see some corrective effect due to the proportional control?
Eventually you will have to design a controller so that essentially all initial error is driven to zero by the end of the first trajectory segment; otherwise, your grasp operation may fail.
Once you get good behavior with feedforward-plus-P control, try experimenting with other variants: P control only; PI control only; and feedforward-plus-PI control.
What to submit: You will submit a single .zip file of a directory with the following contents:
- A file called README.txt or README.pdf. This file should briefly explain your software and your results. If you needed to follow a different approach to solve the problem than the one described above, explain why and explain your solution method. If you encountered anything surprising, or if there is something you still don't understand, explain it.
- Your commented code in a directory called "code." Your code should be lightly commented, so it is clear to the reader what the code is doing. No need to go overboard, but keep in mind your reviewer may not be fluent in your programming language. Your code comments must include an example of how to use the code. Only turn in functions that you wrote or modified; you don't need to turn in other MR functions that your code uses. If your code is in MATLAB or Python, just turn in the text files with your functions. If your code is in Mathematica, turn in (a) your .nb notebook file and (b) a .pdf printout of your code, so a reviewer can read your code without having to have the Mathematica software. Ideally your code would automatically generate a .csv file, but it is also acceptable if it simply prints out the comma-separated values, which then must be copy-and-pasted into a text editor to create the .csv file.
- A directory called "results" with the results of your program. This directory should contain two directories: one titled "best" and one titled "overshoot." The directory "best" should contain the results using a well-tuned controller, either feedforward-plus-P or feedforward-plus-PI. The convergence exhibited by the controller does not necessarily have to be fast, but the motion should be smooth, with no overshoot, and very little error by partway through trajectory segment 1. The directory "overshoot" should contain the results using a less-well-tuned controller, one that exhibits overshoot and a bit of oscillation. Nonetheless, the error should be eliminated before the end of trajectory segment 1. Your controller for these results will likely be feedforward-plus-PI or just PI. In each of the two directories, give:
- A very brief README.txt or README.pdf file that indicates the controller used or any other information about the results.
- A log file showing the program being called with the input.
- The V-REP .csv file produced by the program.
- The animation (a video) of your .csv file being animated by the V-REP scene.
- The data file produced by your program.
- A plot of the six elements of as a function of time, showing the convergence to zero.
Project grading. Your project will be graded on the clarity and correctness of your README files and your code. Your "results" directories will be graded on their correctness, including whether your error plots show reasonable convergence to zero and the quality of your videos.
If you succeed in this project, congratulations! You have integrated concepts from all five previous Modern Robotics courses in a fairly sophisticated piece of software.
Alternative Solution Methods
You could imagine other approaches to solving the mobile manipulator pick-and-place problem, instead of just planning a trajectory for the end-effector and using feedback control to track it. For example, you could use an obstacle-avoiding motion planner to plan a reference trajectory for the entire robot, not just the end-effector. You could incorporate joint limits for the robot arm. You could use a weighted pseudoinverse, instead of the standard pseudoinverse, to indicate a preference to use the wheel or joint motions. You could actively avoid singularities of the arm. You could restrict motion of the mobile base to trajectory segments 1 and 5, and use only the robot arm for trajectories 2, 4, 6, and 8.
If you have other ideas on better ways to approach the mobile manipulation problem, feel free to mention them in the discussion prompt or your main README file.













![{\displaystyle T_{sb}(q)=\left[{\begin{array}{cccc}\cos \phi &-\sin \phi &0&x\\\sin \phi &\cos \phi &0&y\\0&0&1&0.0963\\0&0&0&1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b47257eb7970f48760d2e63f234ada12b6c2b441)

![{\displaystyle T_{b0}=\left[{\begin{array}{cccc}1&0&0&0.1662\\0&1&0&0\\0&0&1&0.0026\\0&0&0&1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b10156ace98a292244209f583368c4de8f50942)
![{\displaystyle M_{0e}=\left[{\begin{array}{cccc}1&0&0&0.033\\0&1&0&0\\0&0&1&0.6546\\0&0&0&1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c9e700700bbd505a17718ed8e8e5499e6208a54)





























![{\displaystyle T_{se}=\left[{\begin{array}{cccc}r_{11}&r_{12}&r_{13}&p_{x}\\r_{21}&r_{22}&r_{23}&p_{y}\\r_{31}&r_{32}&r_{33}&p_{z}\\0&0&0&1\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee8bd2c5d74f359729ec0636914dec7bdca4ca33)
![{\displaystyle {\mathcal {V}}(t)=[{\text{Ad}}_{X^{-1}X_{d}}]{\mathcal {V}}_{d}(t)+K_{p}X_{\text{err}}(t)+K_{i}\int _{0}^{t}X_{\text{err}}({\text{t}})d{\text{t}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74fbaf5a58edd66aed04fba0a0052f423114dbff)











![{\displaystyle [X_{\text{err}}]=\log(X^{-1}X_{d})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98acd3551469051e4abf19cd8c910884a264f14f)


![{\displaystyle [{\mathcal {V}}_{d}]=(1/\Delta t)\log(X_{d}^{-1}X_{d,{\text{next}}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/120ecbaa9a68f82f69d08793b5efe6036df4b59e)

![{\displaystyle \left[{\begin{array}{c}u\\{\dot {\theta }}\end{array}}\right]=J_{e}^{\dagger }(\theta ){\mathcal {V}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b58a5ea9c22a123198fb9355e2ef000f06ad9f1d)



![{\displaystyle T_{se}=\left[{\begin{array}{cccc}0&0&1&0\\0&1&0&0\\-1&0&0&0.5\\0&0&0&1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45dda1e0d9ac53357a867370bff45c902fe2a3a)