Voltage and Current Dividers

Voltage Division

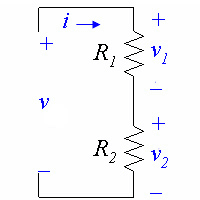
When we have a voltage across a string of resistors connected in series, the voltage across the entire string will be divided up among the resistors. We can express the voltage across a single resistor as a ratio of voltages and resistances, without ever knowing the current.

In the circuit above,

${\frac {v_{1}}{v}}={\frac {R_{1}}{R_{1}+R_{2}}}$

or

$v_{1}={\frac {R_{1}}{R_{1}+R_{2}}}v$

We can generalize this equation for $N$ resistors in series with the equation:

$v_{k}={\frac {R_{k}}{R_{1}+R_{2}+\cdot \cdot \cdot +R_{N}}}v$

where $v_{k}$ is the voltage across resistor $k$ and $v$ is the voltage across the whole string of resistors.

Current Division

Resistors in parallel divide up the current. When we have a current flowing through resistors in parallel, we can express the current flowing through a single resistor as ratio of currents and resistances, without ever knowing the voltage.

In the circuit above

${\frac {i_{1}}{i}}={\frac {R_{2}}{R_{1}+R_{2}}}$

or

$i_{1}={\frac {R_{2}}{R_{1}+R_{2}}}i$

where $i$ is the current flowing through all the resistors. Note that the numerator on the right is R2, not R1. Remember that a larger resistance will carry a smaller current.

We can generalize the equation for $N$ resistors in parallel with the equation:

$i_{k}={\frac {\frac {1}{R_{k}}}{{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdot \cdot \cdot +{\frac {1}{R_{N}}}}}i$

where $i_{k}$ is the current flowing through resistor $k$ and $i$ is the current flowing through all the resistors.

Practice Problems

Problem 1

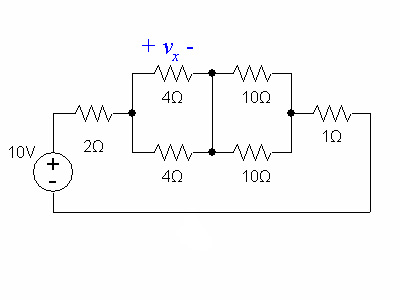
Use voltage division to find $v_{x}$ in the circuit below:

click here for the solution

Problem 2

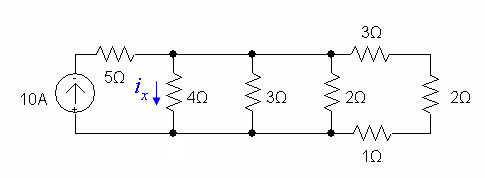
Simplify the circuit and then use current division to find $i_{x}$ in the circuit below:

click here for the solution