RC and RL Exponential Responses
Summary of Equations
| Discharging | Charging | Time Constant | |
|---|---|---|---|
| Capacitor | |||
| Inductor |
RC Circuits
Charging
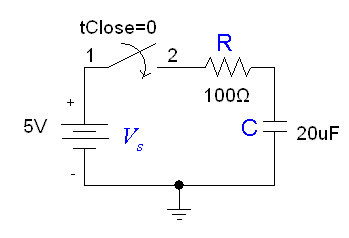
If the capacitor is initially uncharged and we want to charge it with a voltage source in the RC circuit:
Current flows into the capacitor and accumulates a charge there. As the charge increases, the voltage rises, and eventually the voltage of the capacitor equals the voltage of the source, and current stops flowing. The voltage across the capacitor is given by:
where , the final voltage across the capacitor.
Discharging
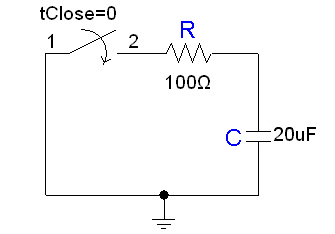
Consider the following circuit:
In the circuit, the capacitor is initially charged and has voltage across it, and the switch is initially open. At time , we close the circuit and allow the capacitor to discharge through the resistor. The voltage across a capacitor discharging through a resistor as a function of time is given as:
where is the initial voltage across the capacitor.
The term RC is the resistance of the resistor multiplied by the capacitance of the capacitor, and known as the time constant, which is a unit of time. The function completes 63% of the transition between the initial and final states at , and completes over 99.99% of the transition at .
The voltage and current of the capacitor in the circuits above are shown in the graphs below, from t=0 to t=5RC. Note the polaritiy—the voltage is the voltage measured at the "+" terminal of the capacitor relative to the ground (0V). A positive current flows into the capacitor from this terminal; a negative current flows out of this terminal.:
| Voltage | Current | |
|---|---|---|
| Charge | 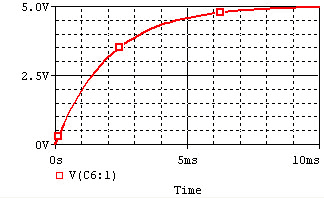 |

|
| Discharge | 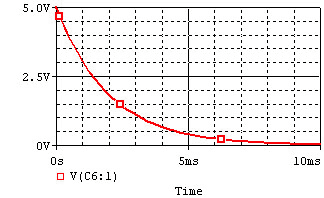 |
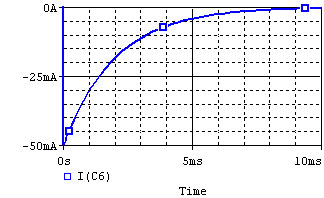
|
Remember that for capacitors, . Note that the current through the capacitor can change instantly at t=0, but the voltage changes slowly.
RL Circuits
Charging
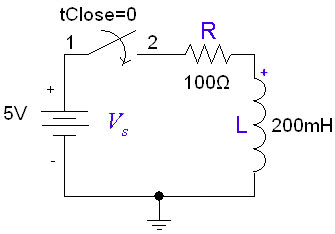
If the inductor is initially uncharged and we want to charge it by inserting a voltage source in the RL circuit:
The inductor initially has a very high resistance, as energy is going into building up a magnetic field. Once the magnetic field is up and no longer changing, the inductor acts like a short circuit. The current at steady state is equal to . Since the inductor is acting like a short circuit at steady state, the voltage across the inductor then is 0. The current through the inductor is given by:
Discharging
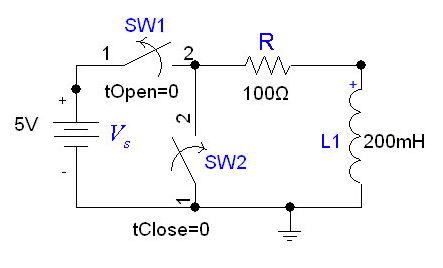
In the following circuit, the inductor initially has current flowing through it; we replace the voltage source with a short circuit at .
After we cut out the voltage source, the voltage across the inductor is , but the higher voltage is now at the negative terminal of the inductor. Thus, . The current flowing through the inductor at time t is given by:
where .
The time constant for the RL circuit is equal to .
The voltage and current of the inductor for the circuits above are given by the graphs below, from t=0 to t=5L/R. The voltage is measured at the "+" terminal of the inductor, relative to the ground. A positive current flows into the inductor from this terminal; a negative current flows out of this terminal:
| Voltage | Current | |
|---|---|---|
| Charge | 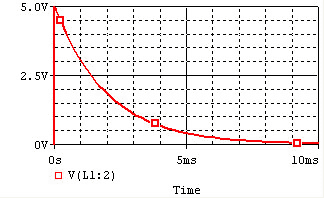 |
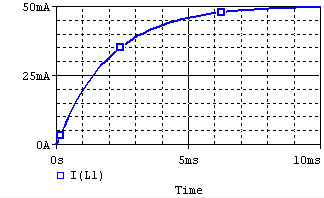
|
| Discharge | 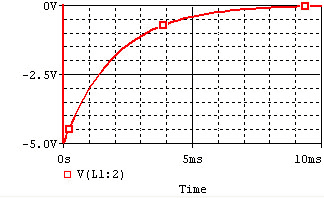 |
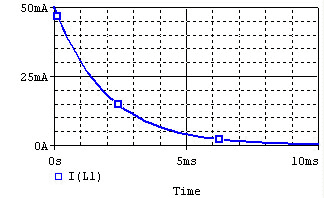
|
Remember that for an inductor, . Note that the voltage across the inductor can change instantly at t=0, but the current changes slowly.
References
Hayt, William H. Jr., Jack E. Kemmerly, and Steven M. Durbin. Engineering Circuit Analysis. 6th ed. New York:McGraw-Hill, 2002.