Evaluating Form Closure Project

This page describes the "Evaluating Form Closure" Project from the Coursera course "Modern Robotics, Course 5: Robot Manipulation and Wheeled Mobile Robots."

Introduction

In this programming assignment, you will write a program to determine if a planar rigid body, subject to a specified set of stationary point contacts, is in form closure.

Your assignment will be graded based on:

• An evaluation of your source code, including its clarity for the reader.
• The correctness of your code's output on two sets of example contacts that you create. You will also provide drawings corresponding to the two cases, showing the feasible twist cone (drawn as centers of rotation) corresponding to the contacts in each case, confirming your code's output.

Program Specification

Left: A six-sided polygon with four stationary contacts acting on it, indicated by the contact normals drawn as arrows. The triangular region labeled $-$ is a rotation-center representation of the feasible twist cone, i.e., the twists the polygon can follow without violating the contact. Right: The same six-sided polygon, but with the direction of the top left contact normal changed. Now there are no feasible twists for the polygon, so it is in form closure.

You will write a program to determine if a planar rigid body, subject to a specified set of stationary point contacts, is in form closure. Your program will likely use linear programming, as described in Chapter 12.1.7 in the book. In MATLAB, the function is called linprog. In Mathematica, it is LinearProgramming. In Python, it is scipy.optimize.linprog.

Important note for Python users: A Coursera student mentioned a bug in an earlier version of linprog, apparently occurring when using the 'simplex' method for solving linear programs where the equality constraints are specified by a matrix that is not full rank. One solution is to use the interior point method by adding the option "method='interior-point'". See the discussion at https://github.com/scipy/scipy/issues/6690.

(Although your program will be written for planar form closure [to allow you to intuitively compare your results to those achieved using graphical methods], it is trivial to extend your program to spatial form closure.)

Your program will take as input a list of stationary point contacts on the body, each specified by the $(x,y)$ contact location and the direction of the contact normal. The contact normal direction should be specified by a single number (the angle of the inward-pointing normal, in degrees or radians, relative to the positive $x$-axis). Ideally the input would be in the form of arguments to your function, or would be read from an external input file that is easily edited.

The output of your program will be binary: the body is either in form closure or not in form closure. If the body is in form closure, it is also recommended that you output the solution to the linear program. This will be a (nonunique) vector $k$ of nonnegative wrench magnitudes at the contacts such that the sum of contact wrenches on the body is zero. (See Example 12.7 in the book.)

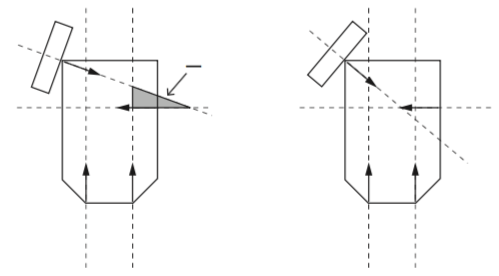
As an example, the image on the right shows a six-sided polygon contacted by four point contacts. In the case on the left, the polygon is not in form closure; there is a cone of feasible twists, as represented by the rotation center region labeled $-$. In the case on the right, the polygon is in form closure, and there is no feasible twist cone; the altered contact normal direction of the top-left contact makes the difference.

Testing Your Program

You will test your program on two sets of contacts, one that yields form closure and one that does not. Ideally the two sets of contacts would differ from each other by a change in just one of the contacts (either its $(x,y)$ location, its contact normal, or both), just as the sets of contacts in the image on this page differ by just one contact. But, I encourage you to come up with your own sets of contacts; don't just use the contacts shown in the image on this page. For each set of contacts, you should draw the feasible twist cone as rotation-center regions, as shown in the image on this page. Your drawings should show the $(x,y)$ coordinate frame, so the reader can understand the coordinates for the contact points, and they should confirm the answers provided by your program.

What to Submit

You will submit a single .zip file with the following contents:

1. Your commented code in a directory called "code." Your code should be lightly commented, so it is clear to the reader what the code is doing. No need to go overboard, but keep in mind your reviewer may not be fluent in your programming language. Your code comments must include an example of how to use the code. You can write your program in any language, provided it is clearly structured, reasonably modular, easy to understand for a reader with no experience in your programming language, and with sufficient comments. Your program can span multiple files, or it can be a single file, if appropriate. If your code is in Mathematica, turn in (a) your .nb notebook file and (b) a .pdf printout of your code, so a reviewer can read your code without having to have the Mathematica software.
2. A directory called "results". In this directory you should have pictures of the two contact cases you used for testing. Each picture should show the $(x,y)$ coordinate frame so the coordinates of the contacts are clear; each picture should show the contact locations and normal directions; and each picture should show the body's feasible twist cone as a region of rotation centers using the graphical methods from Chapter 12.1. If the body is in form closure, then there is no twist cone. This directory should also have the output logs of your program when given the input for these two cases, showing your program being called with the input corresponding to your pictures and showing the output (form closure or not form closure).
3. (OPTIONAL) A plain text file called "README.txt" or other explanatory file. This has any other information that may help the reviewer understand your submission.