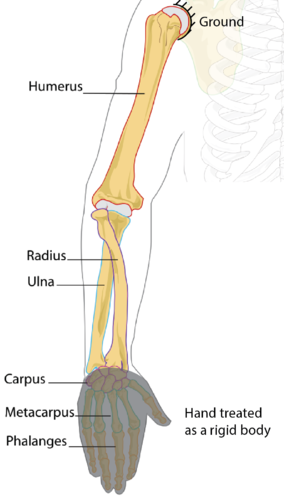
DOF of the Human Arm
Always remember: Grubler's formula is just an expression of the concept that the number of degrees of freedom of a mechanism is equal to the number of degrees of freedom of the rigid bodies minus the number of independent constraints on the motion of those bodies. So even if the mechanism does not have traditional joints (spherical, revolute, etc.), you may still be able to count the number of degrees of freedom.
Part 1: How many degrees of freedom does a typical human arm have, from the shoulder to just past the wrist? Assume that the (x,y,z) position of the center of the shoulder joint is stationary (e.g., the shoulder can't "hunch" upward), and don't count any degrees of freedom in the hand (pretend the hand is just a rigid body). We want to know the number of degrees of freedom of the joints at the shoulder, the elbow, and the wrist.
Try solving the problem two ways:
- Add up the joint freedoms as you move your shoulder, elbow, and wrist around.
- Put your hand on a table at a fixed location, with your elbow bent. (We are avoiding the singularity where your elbow is locked out straight!) Without moving your hand or the (x,y,z) position of your shoulder, how many motion freedoms does your arm still have? How many constraints did you place on your arm when you fixed your hand (a rigid body) at a particular configuration on the table? Given these, what must be the number of degrees of freedom of your arm when you don't have constraints on your hand's position?
Your answers from methods (1) and (2) should be the same.
Is your answer for the number of dof larger, smaller, or the same as the number of dof of a rigid body in space? Why might that matter?
Part 2: One last thing you could think about: The human arm has one effectively rigid bone in the upper arm (the humerus) and two rigid bones in the forearm (the radius and the ulna), as shown in the image to the right. And, since we're only talking about the DOF of the arm, you can think of the hand as a rigid body. Given the four rigid bodies of the arm (humerus, radius, ulna, hand), and your answer to the number of degrees of freedom of the arm, how many constraints on the motions of the rigid bodies must be provided by joints? (These joints are between the four rigid bodies, and between the humerus and the shoulder socket, or "ground.")