A* Graph Search Project

This page describes the A* Graph Search Project from the Coursera course "Modern Robotics, Course 4: Robot Motion Planning and Control."

Introduction

In this programming assignment, you will implement A* search. Given a graph, the start node, and the goal node, your program will search the graph for a minimum-cost path from the start to the goal. Your program will either return a sequence of nodes for a minimum-cost path or indicate that no solution exists.

Your assignment will be graded based on:

• An evaluation of your source code, including its clarity for the reader.
• The correctness of your code's output, according to the specification below.
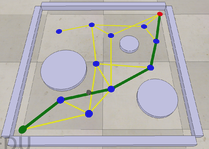
• The correctness of your CoppeliaSim screenshot of your solution.

Downloading and testing the needed CoppeliaSim files

First you should read about the CoppeliaSim simulator scene "CSV Motion Planning Kilobot" (Scene 5) on the Modern Robotics wiki. You should then download the associated .ttt CoppeliaSim scene file and the .zip file with sample input to the scene. When you extract the .zip file, you will have a folder with four files inside: nodes.csv (describing the nodes of the graph), edges.csv (describing the edges of the graph), path.csv (describing a solution path), and obstacles.csv (describing cylindrical obstacles, just for visualization purposes). Read the wiki (and the files themselves, which have comments) for more information on the formats of these files.

Play the scene in CoppeliaSim and choose the folder with the four files as the input. When you press the "play" button on the interface, you will see a display of the graph, the obstacles, and a path through the graph. You will also see a small mobile robot, a swarm robot called a kilobot, travel along the path. Make sure you can do this before moving on with the rest of the assignment.

In this assignment, you will create a program that implements A* search to find a minimum-cost path through an undirected graph. You will use the CoppeliaSim scene to visualize the graph and the solution path found by your program. Although the nodes of your graph are assigned (x,y) coordinates in a plane for visualization purposes (and the solution is animated by a planar mobile robot), the A* graph search you will implement is for fully general undirected weighted graphs. As such, the nodes could represent configurations in arbitrary C-spaces, such as the six-dimensional C-space of the rigid chassis of a spacecraft flying among asteroids. We visualize the nodes of the graph as points in a plane, for simplicity.

Writing your program

You will write a program that takes two files as input, nodes.csv and edges.csv, and produces a single file as output, path.csv. You can test your program on the nodes.csv and edges.csv file that you downloaded from the Modern Robotics wiki, to make sure that your code is working properly.

The sample nodes.csv and edges.csv files on the wiki have comments in them. All lines beginning with the hashtag character # are ignored. You can write your software to handle comments such as these, or you can assume that the input files have no comments. In the latter case, you will need to delete the comments from the nodes.csv and edges.csv file before using them to test your code.

You can write your program in any language, provided your program is clearly structured, reasonably modular, easy to understand for a reader with no experience in your programming language, and with sufficient comments. Your program can span multiple files, or it can be a single file, if appropriate.

If there are N nodes, numbered 1...N in nodes.csv, you can assume that node 1 is the start node and node N is the goal node. Your output file path.csv should be a single line of the form

 1, node2, node3, ..., N

indicating that the solution path goes from nodes numbered 1, to node2, to node3, etc., finally to N. Your program must find the proper node numbers for node2, node3, etc. The solution path should minimize the sum of the edge costs among all possible paths from node 1 to node N, where the edge costs are given in the edges.csv file. If there is no solution, your output file can be simply

 1

indicating that the robot does not go anywhere.

To see the results of your planner, call the CoppeliaSim scene with the nodes.csv and edges.csv file you used as input, the path.csv file that your program wrote as output, and an obstacles.csv file (which is not needed by your program). The obstacles .csv file can be empty if you don't want to visualize obstacles.

This page has information on writing csv files in Python, MATLAB, and Mathematica.

Data structures, algorithms, and computational efficiency

This project is a more extensive programming project than you have done before in the Coursera Modern Robotics specialization. Even if you have not had a lot of programming experience, you should still be able to complete the project based on the A* description in the book.

You will have to make decisions about how to implement data structures such as OPEN, CLOSED, the graph edges, the past costs, and the search trees. You will also have to decide how to implement certain algorithms on these data structures, such as inserting nodes into the sorted list OPEN. Decisions you make about this will affect the efficiency of your implementation (e.g., the amount of memory needed to store your data, or the amount of time it takes to perform certain operations). However, your assignment will not be graded on efficiency. You are free to simply use two-dimensional matrices and one-dimensional arrays to represent your data and to use inefficient algorithms on them (e.g., for inserting nodes in the sorted list OPEN).

For large search problems, efficiency matters, but this is not a computer science course, and there are no prerequisites in data structures or algorithms, so our focus is on understanding the ideas of A* graph search and correctness of the implementation, not efficiency.

You may also have to choose a maximum number of nodes for your implementation. You can make any reasonable assumption (e.g., at least 100 nodes).

What to submit

Once your program is producing correct output, you are ready to assemble your documents for submission. You will submit a single .zip file of a directory with the following contents:

1. Your commented code in a directory called "code." Your code should be lightly commented, so it is clear to the reader what the code is doing. No need to go overboard, but keep in mind your reviewer may not be fluent in your programming language. Your code comments must include an example of how to use the code. You can write your program in any language, provided it is clearly structured, reasonably modular, easy to understand for a reader with no experience in your programming language, and with sufficient comments. Your program can span multiple files, or it can be a single file, if appropriate. If your code is in Mathematica, turn in (a) your .nb notebook file and (b) a .pdf printout of your code, so a reviewer can read your code without having to have the Mathematica software.
2. A directory called "results" with four files in it: nodes.csv, edges.csv, obstacles.csv, and path.csv. The nodes.csv file and edges.csv file should be readable by your program. The nodes.csv file should be identical to the sample nodes.csv file you downloaded, except you can delete the comments if your code does not handle files with comments. The edges.csv file should also be identical to the sample edges.csv file (perhaps without the comments) except the edge from node 4 to node 7 should be deleted, to change the graph from the original graph. The obstacles.csv file should be identical to the sample file you downloaded from the wiki. The path.csv file should be the unmodified output of your program when taking nodes.csv and edges.csv as input.
3. A CoppeliaSim screenshot of your solution path on the graph. The graph among the obstacles should be clearly visible.
4. (OPTIONAL) A plain text file called "README.txt" or other explanatory file. This has any other information that may help the reviewer understand your submission.