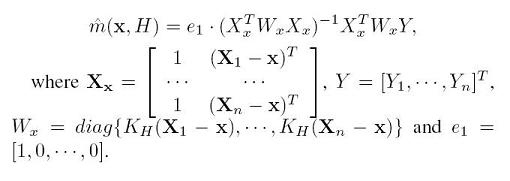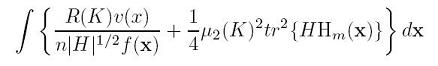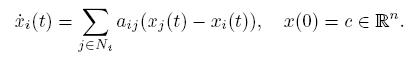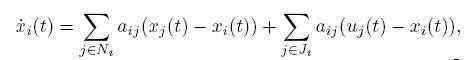Swarm Robot Theoretical Research
Introduction
In this theoretical research part, we will introduce project related research papers and provide with a brief explanation for main ideas, algorithms, for papers. Major mathematical expressions, or equations, for each paper will be presented. Also, there will be link for original papers.
Bibliography Report
i. Distributed Kriged Kalman Filter for Spatial Estimation
Author: Jorge Cort´es
This paper considers robotic sensor networks performing spatially-distributed estimation tasks. A robotic sensor network takes successive point measurements, in an environment of interest, of a dynamic physical process model as a spatio-temporal random field. The paper introduces Distributed Kriged Kalman Filter for predictive inference of the random field and its gradient.
Physical process as spatio-temporal Gaussian random field Z:
![]()
Mean: ![]()
Robotic network of n agents {p1, … , pn} in Rd:
![]()
Number of network agent n is a priori known to everybody
Spatial Prediction:
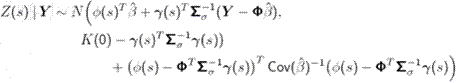
For spatial prediction, simple kriging and parameter estimation are combined. Similar procedure can be carried out for sequential estimation, when measurements are taken successively.
Link for this paper: http://tintoretto.ucsd.edu/jorge/publications/data/2007_Co-tac.pdf
ii. Data Assimilation via Error Subspace Statistical Estimation
Author: P. F. J. LERMUSIAUX
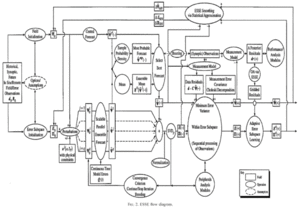
This paper introduces an efficient scheme for data assimilation in nonlinear ocean atmosphere models via ESSE approach. The main goal of this paper is to develop the basis of a comprehensive DA scheme for the estimation and simulation of realistic geophysical fields. The main concept, or whole flow, of this paper is depicted as a figure below:
Predictability and Model errors: ![]()
Link for this paper: http://web.mit.edu/pierrel/www/Papers/mwr2_99.pdf
iii. Parameter Uncertainty in Estimation of Spatial Functions: Bayesian Analysis
Author: Peter K. Kitanidis
This paper analyzes the problem of uncertain parameter and its effect on inference of spatial functions with Bayesian analysis. Parameters are treated as random variables with probability distributions reflecting the known facts. The analysis shows how prior information about the parameters may be combined in the analysis with information in the sample. The result provides insight into the applicability of maximum likelihood versus restricted maximum likelihood parameter estimation, and conventional linear versus kriging estimation.
General Model: 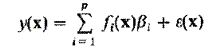
x: the vector of spatial coordinates of the point where y is sampled
β: (generally unknown) parameter
fi(x): known functions of the spatial coordinates
ε(x): zero-mean spatial random function; existed random measurement error would be incldued
Prediction model: ![]()
Prediction model may be defined as finding the PDF
y0: a vector of unknown point or weighted-average values of given observation y
X0: the matrix of deterministic effects for y0
Download this paper: parameter uncertainty in estimation of spatial functions, bayesian analysis
iv. Adaptive Sampling Using Feedback Control of an Autonomous Underwater Glider Fleet
Author: Edward Fiorelli, Pradeep Bhatta, Naomi Ehrich Leonard
This paper presents strategies for adaptive sampling using Autonomous Underwater Vehicle, simply AUV, fleets. The main idea is the use of feedback that integrates distributed measurements into a coordinated mission planner. The cooperative gradient climbing is intended to allow the glider fleet make use of observational data and therefore overcome errors in forecast data.
Link for this paper: http://www.princeton.edu/~naomi/uust03FBLSp.pdf
v. Cooperative Control of Mobile Sensor Networks: Adaptive Gradient Climbing in a Distributed Environment
Author: Petter Ögren, Edward Fiorelli,and Naomi Ehrich Leonard
This paper presents a stable control strategy for groups of vehicles to move and reconfigure cooperatively in response to a sensed and distributed environment. It focuses on gradient climbing missions in which the mobile sensor network seeks out local maxima or minima in the environmental field. The network can adapt its configuration in response to the sensed environment in order to optimize its gradient climb.
Link for this paper: http://www.princeton.edu/~naomi/OgrFioLeoTAC04.pdf
vi. Adaptive Sampling for Estimating a Scalar Field using a Robotic Boat and a Sensor Network
Author: Bin Zhang and Gaurav S. Sukhatme
This paper shows an adaptive sampling algorithm for a mobile sensor network to estimate a scalar field. The data from robots are used to estimate the scalar field. It also explains how the IMSE and the second derivatives of the phenomenon investigated are related to each other. In this paper, the estimation is based on local linear regression, the non-parametric regression where the predictor does not have the fixed form but the predictor is going to be constructed by the information gathered from the data. Of many non parametric estimators, this paper deals with the Kernel estimator.
Y = scalar response
m(x) = function to be estimated
Link for this paper: http://cres.usc.edu/pubdb_html/files_upload/524.pdf
vii. Consensus Filters for Sensor Networks and Distributed Sensor Fusion
Author: Reza Olfati-Saber, Jeff S. Shamma
This paper introduces a distributed filter that allows the nodes of a sensor network to track the average of n sensor measurements using an average consensus based distributed filter called consensus filter. This consensus filter is very important in solving a data fusion problem. The objective of this algorithm mentioned in this paper is to design the dynamics of a distributed low-pass filter that takes u as an input and y = x as the output whose property is that asymptotically all nodes of the network reach an ε-consensus regarding the value of signal r(t) in all time t. This paper also introduces the various properties of this distributed filter.
Link for this paper: http://www.nt.ntnu.no/users/skoge/prost/proceedings/cdc-ecc05/pdffiles/papers/1643.pdf