Difference between revisions of "Kirchhoff's Current and Voltage Laws"
| (52 intermediate revisions by 4 users not shown) | |||
| Line 2: | Line 2: | ||
==Kirchhoff's Current Law and Nodal Analysis== |
==Kirchhoff's Current Law and Nodal Analysis== |
||
Kirchhoff's Current Law (KCL) says that the current going into a junction or node is equal to the current going |
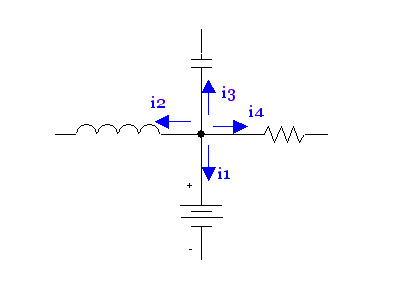
Kirchhoff's Current Law (KCL) says that the current going into a junction or node is equal to the current going out of a node. In other words, the sum of the currents entering the node must be zero (if we consider currents leaving the node to be a negative current entering the node). Consider the following diagram: |
||
[[Image:kirchhoffs_current_law_node_diagram. |
[[Image:kirchhoffs_current_law_node_diagram.gif]] |
||
For the node '''A''' in the center, ''i1'' and ''i2'' are entering the node, and ''i3'' and ''i4'' are leaving the node. We would write: |
For the node '''A''' in the center, ''i1'' and ''i2'' are entering the node, and ''i3'' and ''i4'' are leaving the node. We would write: |
||
| Line 12: | Line 12: | ||
Note that ''i7'' is equal to ''i2''; we can prove this by analyzing node '''B'''. We can also treat everything between node '''C''' and '''D''' as one big node, and conclude that ''i5'' is equal to ''i6'' without having to know the value of any of the currents within. |
Note that ''i7'' is equal to ''i2''; we can prove this by analyzing node '''B'''. We can also treat everything between node '''C''' and '''D''' as one big node, and conclude that ''i5'' is equal to ''i6'' without having to know the value of any of the currents within. |
||
When solving for the currents in a real problem, we can choose arbitrarily in which direction the arrows point. If |
When solving for the currents in a real problem, we can choose arbitrarily in which direction the arrows point. If the current flows opposite to the direction of our arrow, the value we obtain after solving for the current will be negative. If you draw ''i4'' as leaving node '''A''' as in the diagram above, then ''i4'' must be entering node '''D'''. |
||
If we had drawn the currents for node '''A''' as following: |
|||
[[Image:kirchhoffs_current_law_node2. |
[[Image:kirchhoffs_current_law_node2.gif]] |
||
Then our node equation looks like: |
Then our node equation looks like: |
||
| Line 22: | Line 22: | ||
<math>i1+i2+i3+i4=0\,</math> |
<math>i1+i2+i3+i4=0\,</math> |
||
Unless all the currents are zero, one or more of the currents must turn out to be negative. The negative currents |
Unless all the currents are zero, one or more of the currents must turn out to be negative. The negative currents flow in the direction opposite from that which the arrow is pointing. |
||
==Kirchhoff's Voltage Law and Loop Analysis== |
==Kirchhoff's Voltage Law and Loop Analysis== |
||
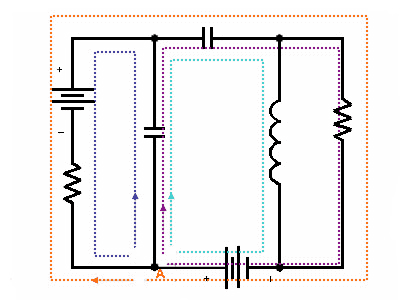
Kirchhoff's Voltage Law (KVL) states that the sum of the voltages around any closed loop is equal to zero. Also, the voltage between any two nodes is the same no matter which path is taken. In the following diagram, it doesn't matter which path you choose(or which direction you go in) to add the voltages of the components from point ''A'' back to point ''A'', they all must add up to zero. |
Kirchhoff's Voltage Law (KVL) states that the sum of the voltages around any closed loop is equal to zero. Also, the voltage between any two nodes is the same no matter which path is taken. In the following diagram, it doesn't matter which path you choose(or which direction you go in) to add the voltages of the components from point ''A'' back to point ''A'', they all must add up to zero. |
||
[[Image:Kirchhoff_voltage_law_loop. |
[[Image:Kirchhoff_voltage_law_loop.gif]] |
||
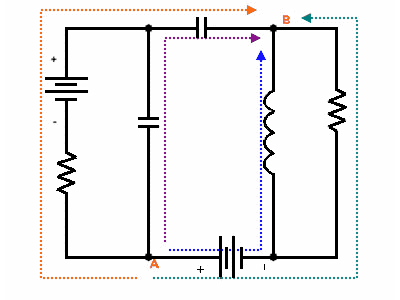
Also, the voltage between any two points does not depend on which path you take. In the following diagram, the voltage between point ''A'' and point ''B'' is the same no matter which path is |
Also, the voltage between any two points does not depend on which path you take. In the following diagram, the voltage between point ''A'' and point ''B'' is the same no matter which path is chosen. |
||
[[Image:kirchhoff_voltage_law_paths. |
[[Image:kirchhoff_voltage_law_paths.gif]] |
||
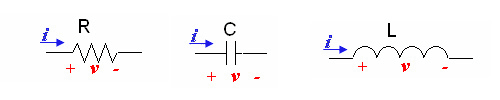
To keep all the positive |
To keep all the positive and negative signs lined up when solving a circuit, we use the following sign convention for the voltage and current for the components: |
||
[[Image:kirchhoff_sign_conventions. |
[[Image:kirchhoff_sign_conventions.gif]] |
||
With the sign convention above, <math>iv > 0</math> means that the element is storing power (for a capacitor or inductor) or dissipating power (for a resistor). If <math>iv < 0 </math>, the element is sourcing, or providing, power. Note that resistors cannot store power (and hence cannot supply power); the energy absorbed by a resistor is lost as heat energy. |
|||
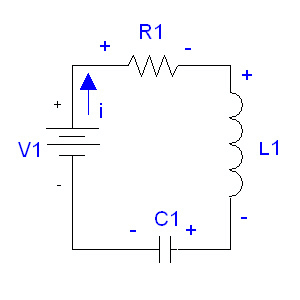
The circuit below shows a battery, resistor, inductor, and capacitor connected in series. |
The circuit below shows a battery, resistor, inductor, and capacitor connected in series. |
||
[[Image:kirchhoff_voltage_law_analysis1. |
[[Image:kirchhoff_voltage_law_analysis1.gif]] |
||
In this circuit, we have chosen to draw the current flowing clockwise and assign the voltages for our components according to our sign |
In this circuit, we have chosen to draw the current flowing clockwise and assign the voltages for our components according to our sign convention. We then add up the voltages of the components, following the loop. It doesn't matter if you go clockwise or counter-clockwise. If you go from a "+" sign to a "-" sign when going around the loop, subtract the voltage across that element. Otherwise, add it. Once you've completed the loop, set the summation equal to zero. |
||
In the example above, if we choose to start in the bottom left corner and move in the clockwise direction, our equation looks like: |
In the example above, if we choose to start in the bottom left corner and move in the clockwise direction, our equation looks like: |
||
| Line 55: | Line 57: | ||
If we had drawn the current going in a counter-clockwise direction, our circuit diagram would look like this: |
If we had drawn the current going in a counter-clockwise direction, our circuit diagram would look like this: |
||
[[Image:kirchhoff_voltage_law_analysis2. |
[[Image:kirchhoff_voltage_law_analysis2.gif]] |
||
Adding up the voltages gives: |
Adding up the voltages gives: |
||
| Line 61: | Line 63: | ||
<math> V_{V1}+V_{R1}+V_{L1}+V_{C1}=0\,</math> |
<math> V_{V1}+V_{R1}+V_{L1}+V_{C1}=0\,</math> |
||
==Solving Problems Using Kirchhoff's Laws== |
|||
If we know that <math>V_{V1}</math> is positive, then <math>V_{R1}+V_{L1}+V_{C1}</math> will turn out to be negative, and we know we have our signs flipped. |
|||
To solve for the currents and voltages in a circuit, simply write all KCL and KVL equations and constitutive laws for each element and solve simultaneously. Note that some KCL and KVL equations are redundant and can be eliminated. |
|||
#Write all KCL equations for each node |
|||
#Write all KVL equations for each loop |
|||
#Write all constitutive equations |
|||
#Solve simultaneous equations |
|||
==Example and Practice Problems== |
==Example and Practice Problems== |
||
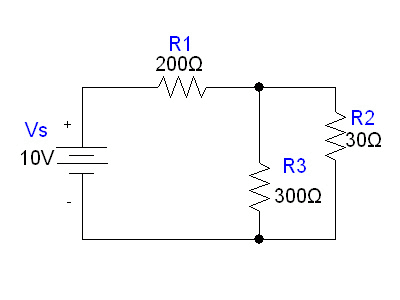
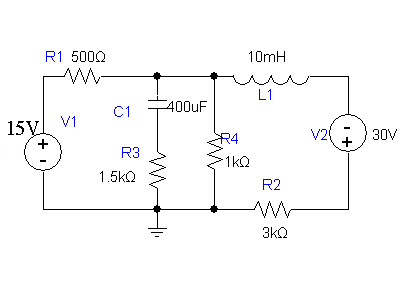
| Line 67: | Line 76: | ||
Find the voltage and current of each resistor at the steady state of the system. |
Find the voltage and current of each resistor at the steady state of the system. |
||
[[Image:kirchhoff_example_1. |
[[Image:kirchhoff_example_1.gif]] |
||
'''Answer''': |
'''Answer''': |
||
At steady state, the capacitor becomes charged and acts like an open circuit, and the inductor acts like a short circuit. Therefore, at steady state, our system is equivalent to: |
At steady state, the capacitor becomes charged and acts like an open circuit, and the inductor acts like a short circuit. Therefore, at steady state, our system is equivalent to: |
||
[[Image:kirchhoff_example1_1. |
[[Image:kirchhoff_example1_1.gif]] |
||
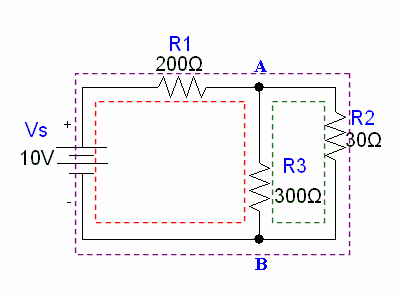
Notice in this circuit, we have two nodes (one at the top and one at the bottom) and three loops (the loop on the left consisting of <math>V_s, R_1,</math> and <math>R_3</math>; the loop on the right consisting of <math>R_2</math> and <math>R_3</math>; and the loop around the entire perimeter, consisting of <math>V_2, R_1,</math> and <math>R_2</math>. |
|||
[[Image:kircchoff_ex1_loopsandnodes.gif]] |
|||
We solve problems like this by writing out the loop equations, node equations, and constitutive laws. Then, we solve the equations simultaneously. |
|||
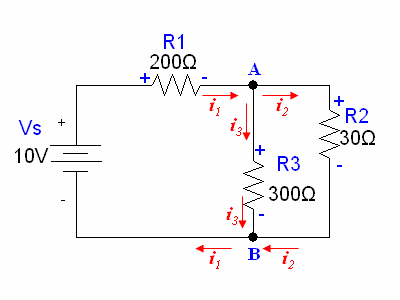
In this example, we draw our current arrows at the nodes as follows: |
|||
[[Image:kirchhoff_ex1_currentarraow.gif]] |
|||
The directions for the currents were chosen arbitrarily. Keep in mind that there is no "wrong" direction when choosing the direction of the arrow, as long as we are consistent with each current's direction. |
|||
We can now write our equations: |
|||
<u>KCL equations</u>: |
|||
Node A: <math>i_1=i_2+i_3</math> |
|||
Node B: <math>i_2+i_3=i_1</math> |
|||
As we can see, the two equations are exactly the same, so we won't be needing both of them. |
|||
<u>KVL equations</u>: |
|||
Loop 1 (left "window pane"): <math>10-200i_1-300i_3=0</math> |
|||
Loop 2 (right "window pane"): <math>300i_3-30i_2=0</math> |
|||
Loop 3 (entire "window frame"): <math>10-200i_1-30i_2=0</math> |
|||
Notice that the equation for ''Loop 3'' is equal to the sum of the equations for ''Loop 1'' and ''Loop 2''. This means that only 2 of the are linearly independent; the third one is redundant. We can choose any two of the three equations to use when solving the system of equations. |
|||
Now we take our node equation and two of our loop equations to make a system of equations (3 equations and 3 unknowns): |
|||
<math>i_1=i_2+i_3</math> |
|||
<math>10-200i_1-300i_3=0</math> |
|||
<math>300i_3-30i_2=0</math> |
|||
Solving the system reveals the currents through each resistor: <math>i_1=0.044A, i_2=0.040A,</math> and <math>i_3=0.004A</math> We then find the voltages across each resistor using the constitutive law for resistors (Ohm's law): <math>V=IR</math>. |
|||
<math>V_1=(0.044)(200)=8.8V</math> |
|||
<math>V_2=(0.040)(30)=1.2V</math> |
|||
<math>V_3=(0.004)(300)=1.2V</math> |
|||
====Alternative Method==== |
|||
First, simplify the network of resistors. The combined resistance of the three resistors is equal to: |
First, simplify the network of resistors. The combined resistance of the three resistors is equal to: |
||
| Line 78: | Line 137: | ||
<math>R_{total}=\frac{(30)(300)}{30+300}+200=227.273\Omega</math> |
<math>R_{total}=\frac{(30)(300)}{30+300}+200=227.273\Omega</math> |
||
The voltage across the resistors is 10V, and using ohm's law, we find that the current going through the circuit is |
|||
The voltage across the resistors is 10V, and using ohm's law, we find that the current going through the circuit is <math>I=10/227.273=0.044A</math>. This is the current flowing through the voltage source ''R1''. Kirchhoff's voltage law tells us that the voltage or ''R2'' and ''R3'' are the same, and the sum of ''R1'' and ''R2'' is equal to 10V. We can find the voltage of ''R1'' by using Ohm's law again: <math>V=(0.044A)(200\Omega)=8.8V</math>. Then ''R2'' and ''R3'' must have <math>10-8.8=1.2V</math> across them, and from that we can calculate that ''R2'' 's current is <math>I=1.2/30=0.04A</math>, and ''R3'' 's current is <math>I=1.2/300=0.004A</math>. Note that the sum of the currents for ''R2'' and ''R3'' is equal to the current in ''R1''. |
|||
<math>i_1=10/227.273=0.044A</math> |
|||
This is the current flowing through the voltage source ''R1''. Kirchhoff's voltage law tells us that the voltage or ''R2'' and ''R3'' are the same, and the sum of ''R1'' and ''R2'' is equal to 10V. We can find the voltage of ''R1'' by using Ohm's law again: |
|||
<math>V=(0.044A)(200\Omega)=8.8V</math> |
|||
Then ''R2'' and ''R3'' must have |
|||
<math>10-8.8=1.2V</math> |
|||
across them, and from that we can calculate that ''R2'' 's current is |
|||
<math>i_1=1.2/30=0.04A</math> |
|||
and ''R3'' 's current is |
|||
<math>i_3=1.2/300=0.004A</math> |
|||
Note that the sum of the currents for ''R2'' and ''R3'' is equal to the current in ''R1''. |
|||
===Example 2=== |
===Example 2=== |
||
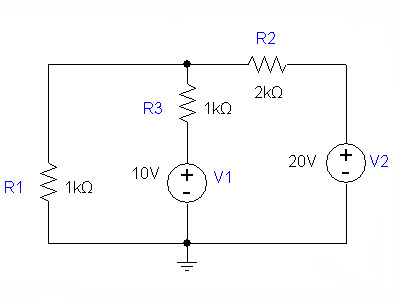
Find the voltage and current of each element in the system. |
Find the voltage and current of each element in the system. |
||
[[Image:kirchhoff_example2. |
[[Image:kirchhoff_example2-1.gif]] |
||
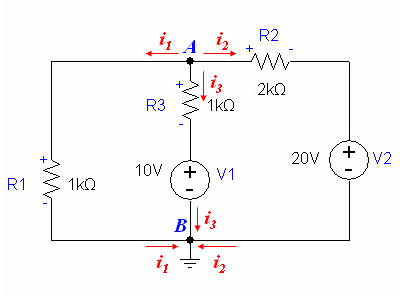
We start by assigning currents to the nodes: |
|||
[[Image:kirchhoff_example2_currentarrow.gif]] |
|||
The we write our '''node equations, loop equations''' and '''constitutive laws'''. |
|||
<u>KCL equations</u>: |
|||
Node A: <math>-i_1-i_2-i_3=0</math> |
|||
Node B: <math>i_1+i_2+i_3=0</math> |
|||
Again, these equations are equivalent, so we only need one of them. |
|||
<u>KVL equations</u>: |
|||
Left-side loop: <math>1000i_1-1000i_3-10=0</math> |
|||
Right-side loop: <math>10+1000i_3-2000i_2-20=0 </math> |
|||
''Beware the sign convention that we use: the voltage of a resistor is high at the end the current is entering into.'' |
|||
These loops already cover the entire circuit. The equation for the "outside frame" will only be the superposition of these two equations, so we omit it. |
|||
The constitutive law for the resistor is <math>V=iR</math>. |
|||
Solving the loop and node equations yields: |
|||
<math>i_1=0.008A</math> |
|||
<math>i_2=-0.006A</math> |
|||
<math>i_3=-0.002A</math> |
|||
Using ''V=iR'', we can find the voltages across each resistor. |
|||
<math> V_{R1}=8V</math> |
|||
<math> V_{R2}=-12V</math> |
|||
<math> V_{R3}=-2V</math> |
|||
The negative value simply means that the voltage is actually higher on at the (-) terminal drawn in the diagram we used to derive our equations. |
|||
The voltage across the voltage source is constant, so: |
|||
<math> V_{V1}=10V</math> |
|||
<math> V_{V2}=20V</math> |
|||
====Alternative Method==== |
|||
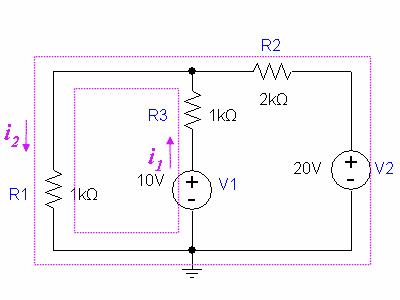
Kirchhoff's current law says that a current flowing into a node also has to flow out of it. If we trace the current's path in a loop, we can also solve for this current. In the figure below, we have two "current loops," and solving for <math>i_1</math> and <math>i_2</math> will give us the currents flowing through each element. The current through <math>V_1</math> and <math>R_3</math> will be the superposition of <math>i_1</math> and <math>i_2</math>. |
|||
[[Image:kirchhoff_example2-2.gif]] |
|||
We can solve this by writing two loop equations using KVL--one for each loop. Note that <math>R3</math> and <math>V1</math> have both <math>i_1</math> and <math>i_2</math> going through them; therefore, the total currents going through <math>R3</math> and <math>V1</math> will be the superposition of <math>i_1</math> and <math>i_2</math>. |
|||
For the loop on the left (in the direction of the current): |
|||
<math>0=V_{V1}-V_{R3}-V_{R1}</math> |
|||
<math>0=V_1-(i_1-i_2)R3-V_{R1}</math> |
|||
<math>0=10-1000(i_1-i_2)-1000(i_1)</math>, |
|||
and for the loop on the right: |
|||
<math>0=V_{V2}-V_{R2}-V_{R3}-V_1</math> |
|||
<math>0=V_{V2}-i_2R2-(i_2-i_1)R_3-V_{V1}</math> |
|||
<math>0=20-2000i_2-1000(i_2-i_1)-10</math> |
|||
Now we have a system of two equations and two unknowns, which is easily solved: |
|||
<math>i_1=8mA</math> and <math>i_2=6mA</math> |
|||
Now we use ohm's law and calculate our voltages: |
|||
<math> V_{V1}=10V</math> |
|||
<math> V_{V2}=20V</math> |
|||
<math> V_{R1}=8V</math> |
|||
<math> V_{R2}=12V</math> |
|||
<math> V_{R3}=2V</math> |
|||
And our currents: |
|||
<math> I_{V1}=6mA</math> |
|||
<math> I_{V2}=2mA</math> |
|||
<math> I_{R1}=8mA</math> |
|||
<math> I_{R2}=6mA</math> |
|||
<math> I_{R3}=2mA</math> |
|||
[[Image:kirchhoff_example2-3.gif]] |
|||
Note that we could also have drawn our loops like this: |
|||
[[Image:kirchhoff_example2-4.gif]] |
|||
In this case, our equations would be: |
|||
for the small loop: |
|||
<math>0=V_{V1}-V_{R3}-V_{R1}</math> |
|||
<math>0=10-1000(i_1)-1000(i_1+i_2)</math> |
|||
and for the big loop: |
|||
<math>0=V_{V2}-V_{R2}-V_{R3}</math> |
|||
<math>0=20-2000i_2-1000(i_2+i_1)</math> |
|||
Solving for <math>i_1</math> and <math>i_2</math>, we find that: |
|||
<math>i_1=2mA</math> |
|||
and |
|||
<math>i_2=6mA</math> |
|||
The current going through <math>R1</math> is equal to <math>i_1+i_2=8mA</math>, which matches our previous answer. |
|||
===Practice Problem 1=== |
|||
Solve for the voltage across and current through each of the components: |
|||
[[Image:Kirchhoff_problem_1.gif]] |
|||
[[kirchhoff practice problem1 solution |Click here for the solution.]] |
|||
===Practice Problem 2=== |
|||
We can solve this by writing two loop equations using KVL. For the loop on the left: |
|||
Solve for the voltage across and current through each of the resistors at time <math>t=0\,</math> and <math>t=\infty</math>. Assume that both the inductor and the capacitor are uncharged in their initial states. |
|||
[[Image:Kirchhoff_problem_2.gif]] |
|||
<math>0=V1 |
|||
[[kirchhoff problem 2 solution|Click here for the solution.]] |
|||
</math> |
|||
Latest revision as of 23:44, 10 January 2011
Kirchhoff's Current Law and Nodal Analysis
Kirchhoff's Current Law (KCL) says that the current going into a junction or node is equal to the current going out of a node. In other words, the sum of the currents entering the node must be zero (if we consider currents leaving the node to be a negative current entering the node). Consider the following diagram:
For the node A in the center, i1 and i2 are entering the node, and i3 and i4 are leaving the node. We would write:
which can also be written as
Note that i7 is equal to i2; we can prove this by analyzing node B. We can also treat everything between node C and D as one big node, and conclude that i5 is equal to i6 without having to know the value of any of the currents within.
When solving for the currents in a real problem, we can choose arbitrarily in which direction the arrows point. If the current flows opposite to the direction of our arrow, the value we obtain after solving for the current will be negative. If you draw i4 as leaving node A as in the diagram above, then i4 must be entering node D.
If we had drawn the currents for node A as following:
Then our node equation looks like:
Unless all the currents are zero, one or more of the currents must turn out to be negative. The negative currents flow in the direction opposite from that which the arrow is pointing.
Kirchhoff's Voltage Law and Loop Analysis
Kirchhoff's Voltage Law (KVL) states that the sum of the voltages around any closed loop is equal to zero. Also, the voltage between any two nodes is the same no matter which path is taken. In the following diagram, it doesn't matter which path you choose(or which direction you go in) to add the voltages of the components from point A back to point A, they all must add up to zero.
Also, the voltage between any two points does not depend on which path you take. In the following diagram, the voltage between point A and point B is the same no matter which path is chosen.
To keep all the positive and negative signs lined up when solving a circuit, we use the following sign convention for the voltage and current for the components:
With the sign convention above, means that the element is storing power (for a capacitor or inductor) or dissipating power (for a resistor). If , the element is sourcing, or providing, power. Note that resistors cannot store power (and hence cannot supply power); the energy absorbed by a resistor is lost as heat energy.
The circuit below shows a battery, resistor, inductor, and capacitor connected in series.
In this circuit, we have chosen to draw the current flowing clockwise and assign the voltages for our components according to our sign convention. We then add up the voltages of the components, following the loop. It doesn't matter if you go clockwise or counter-clockwise. If you go from a "+" sign to a "-" sign when going around the loop, subtract the voltage across that element. Otherwise, add it. Once you've completed the loop, set the summation equal to zero.
In the example above, if we choose to start in the bottom left corner and move in the clockwise direction, our equation looks like:
or if we go in the counter-clockwise direction, we get:
which is the same thing.
If we had drawn the current going in a counter-clockwise direction, our circuit diagram would look like this:
Adding up the voltages gives:
Solving Problems Using Kirchhoff's Laws
To solve for the currents and voltages in a circuit, simply write all KCL and KVL equations and constitutive laws for each element and solve simultaneously. Note that some KCL and KVL equations are redundant and can be eliminated.
- Write all KCL equations for each node
- Write all KVL equations for each loop
- Write all constitutive equations
- Solve simultaneous equations
Example and Practice Problems
Example 1
Find the voltage and current of each resistor at the steady state of the system.
Answer: At steady state, the capacitor becomes charged and acts like an open circuit, and the inductor acts like a short circuit. Therefore, at steady state, our system is equivalent to:
Notice in this circuit, we have two nodes (one at the top and one at the bottom) and three loops (the loop on the left consisting of and ; the loop on the right consisting of and ; and the loop around the entire perimeter, consisting of and .
We solve problems like this by writing out the loop equations, node equations, and constitutive laws. Then, we solve the equations simultaneously.
In this example, we draw our current arrows at the nodes as follows:
The directions for the currents were chosen arbitrarily. Keep in mind that there is no "wrong" direction when choosing the direction of the arrow, as long as we are consistent with each current's direction.
We can now write our equations:
KCL equations:
Node A:
Node B:
As we can see, the two equations are exactly the same, so we won't be needing both of them.
KVL equations:
Loop 1 (left "window pane"):
Loop 2 (right "window pane"):
Loop 3 (entire "window frame"):
Notice that the equation for Loop 3 is equal to the sum of the equations for Loop 1 and Loop 2. This means that only 2 of the are linearly independent; the third one is redundant. We can choose any two of the three equations to use when solving the system of equations.
Now we take our node equation and two of our loop equations to make a system of equations (3 equations and 3 unknowns):
Solving the system reveals the currents through each resistor: and We then find the voltages across each resistor using the constitutive law for resistors (Ohm's law): .
Alternative Method
First, simplify the network of resistors. The combined resistance of the three resistors is equal to:
The voltage across the resistors is 10V, and using ohm's law, we find that the current going through the circuit is
This is the current flowing through the voltage source R1. Kirchhoff's voltage law tells us that the voltage or R2 and R3 are the same, and the sum of R1 and R2 is equal to 10V. We can find the voltage of R1 by using Ohm's law again:
Then R2 and R3 must have
across them, and from that we can calculate that R2 's current is
and R3 's current is
Note that the sum of the currents for R2 and R3 is equal to the current in R1.
Example 2
Find the voltage and current of each element in the system.
We start by assigning currents to the nodes:
The we write our node equations, loop equations and constitutive laws.
KCL equations:
Node A:
Node B:
Again, these equations are equivalent, so we only need one of them.
KVL equations:
Left-side loop:
Right-side loop:
Beware the sign convention that we use: the voltage of a resistor is high at the end the current is entering into.
These loops already cover the entire circuit. The equation for the "outside frame" will only be the superposition of these two equations, so we omit it.
The constitutive law for the resistor is .
Solving the loop and node equations yields:
Using V=iR, we can find the voltages across each resistor.
The negative value simply means that the voltage is actually higher on at the (-) terminal drawn in the diagram we used to derive our equations.
The voltage across the voltage source is constant, so:
Alternative Method
Kirchhoff's current law says that a current flowing into a node also has to flow out of it. If we trace the current's path in a loop, we can also solve for this current. In the figure below, we have two "current loops," and solving for and will give us the currents flowing through each element. The current through and will be the superposition of and .
We can solve this by writing two loop equations using KVL--one for each loop. Note that and have both and going through them; therefore, the total currents going through and will be the superposition of and .
For the loop on the left (in the direction of the current):
,
and for the loop on the right:
Now we have a system of two equations and two unknowns, which is easily solved:
and
Now we use ohm's law and calculate our voltages:
And our currents:
Note that we could also have drawn our loops like this:
In this case, our equations would be:
for the small loop:
and for the big loop:
Solving for and , we find that:
and
The current going through is equal to , which matches our previous answer.
Practice Problem 1
Solve for the voltage across and current through each of the components:
Practice Problem 2
Solve for the voltage across and current through each of the resistors at time and . Assume that both the inductor and the capacitor are uncharged in their initial states.