Design and Control of a Pantograph Robot
Overview
The goal of this project was to design and build a 2-DOF Pantograph Robot. The user would be able to specify and X and Y location for the end point of the pantograph, along with different paths that the robot arm could take. The basic circuit design and computer code was taken from the High Speed Motor Control project and adapted to work with our robot design.
Kinematics
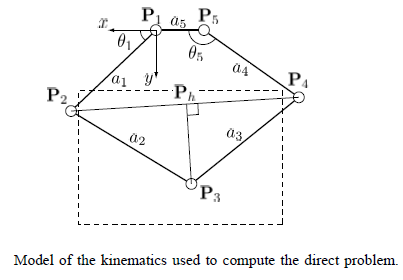
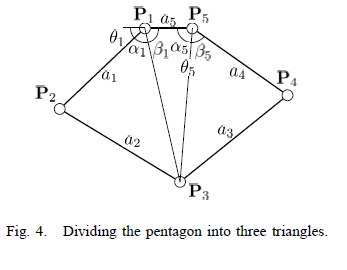
The kinematics for our robot design were derived from The Pantograph Mk. II - A Haptic Instrument. The forward and inverse kinematics as used in the MATLAB program are shown below, along with diagrams from the paper showing how the reference frames are defined in our setup. These angles are all calculated in radians, other parts of the programs convert this to degrees for graphing and user interfaces. The full programs can be found in the zip files below.
Forward Kinematics
x2 = L1 * cos(theta); y2 = L1 * sin(theta); y4 = L4 * sin(alpha); x4 = L4 * cos(alpha) - L5; two_to_four = sqrt((x2-x4).^2 + (y2-y4).^2); two_to_h = (L2^2 - L3^2 + two_to_four.^2) ./ (2 * two_to_four); yh = y2 + (two_to_h./two_to_four).*(y4-y2); xh = x2 + (two_to_h./two_to_four).*(x4-x2); three_to_h = sqrt(L2^2 - two_to_h.^2); x3 = xh + (three_to_h./two_to_four) .* (y4-y2); y3 = yh - (three_to_h./two_to_four) .* (x4-x2);
Inverse Kinematics
L13 = sqrt(x3.^2+y3.^2); L53 = sqrt((x3+L5).^2 + y3.^2); alphaOne = acos((L1.^2 + L13.^2 - L2.^2)./(2.*L1.*L13)); betaOne = atan2(y3,-x3); thetaOne = pi - alphaOne - betaOne; alphaFive = atan2(y3,x3+L5); betaFive = acos((L53.^2 + L4.^2 - L3.^2)./(2.*L53.*L4)); thetaFive = alphaFive + betaFive;
Mechanical Design
Circuit Design
The complete circuit schematic for the current robot setup is displayed to the right. A brief description of the components in the circuit and what they do follows.
This is essentially one smaller circuit repeated for the second motor. Each motor is powered by an L298N H-bridge amplifier which is powered by 12 volts currently. These amplifiers are capable of sending out four different signals, however in this application the matching inputs and outputs are connected in parallel in order to increase the available current.
The PIC sends three signals to each H-bridge, one for each motor lead and an enable signal that activates the amplifier. These signals pass through 4N27 optoisolators to shield the motors from signal noise.
Each motor encoder is connected to an LS7083 encoder counter chip to allow the PIC to keep track of the motor angle in order to control the position of the end effector. This connection is made through a DB9 connector that interfaces with the plug attached to each motor.
There are two hall effect sensors that are mounted on the robot base and connected to the PIC. These allow the user to set the position of the arms by manually moving them at the beginning of the program until they are tripped by small magnets mounted on the robot arms.
The PC communicates with the PIC via RS232 using a MATLAB program. This allows the robot arm to be completely controlled by a PC once the program is loaded onto the PIC chip.
Parts List
| Electrical Components Needed. | Quantity | Data Sheets |
|---|---|---|
| PIC 32 on NU32 board | 1 | Introduction to the PIC32 |
| H-bridges L298 | 2 | data sheet |
| Optoisolators 4N27 | 6 | data sheet |
| Quadrature Up/Down decoders LS7083 | 2 | data sheet |
| Hall Effect Sensors | 2 | Hall Effect Sensor |
| 35V 9A Schottkey Diodes 90SQ035-ND | 8 | data sheet |
| Harmonic Drive RH-8D-3006 Actuator with 100:1 gear ratio and 1000 count per revolution encoder | 2 | data sheet |
| Power Supply | 1 | N/A |