VPOD 3DOF Vibratory Device

Nondimensional 3DOF Bouncing Ball Simulator

Introduction

The Nondimensional 3DOF Bouncing Ball Simulator is a simple Matlab program meant to mimic the behavior of a bouncing ball on a vibratory device capable of sinusoidal motion in three degrees, such as the VPOD. The simulator uses a numerical method in which the equations of motion describing the ball's flight are determined from the state variables of the previous impact. The program uses a binary search to locate the time at which the ball's position in the x,z plane is equal to that of the oscillating bar. In short, it calculates the intersection of a parabola with a sinusoid, uses a simple impact model to compute the new state variables, and repeats this computation as many times as desired. The equations of motion for the oscillating bar are as follows:

$x(t)=A_{x}sin(\omega _{x}t+\phi _{x})\,$

$z(t)=A_{z}sin(\omega _{z}t+\phi _{z})\,$

$\theta (t)=A_{\theta }sin(\omega _{\theta }t+\phi _{\theta })\,$

where A_x, A_z, A_theta represent the maximum x, z, and angular displacements of the bar's motion. The key input variables are the three position amplitudes, three frequencies, and three phase angles, as well as coefficients of restitution in the normal and tangential directions.

Quick Start

In order to run the simulator, first download the Matlab files by clicking on the link below:

Download the simulator.

Description of Functions

The zipped folder contains 6 m-files:

• bBallSim - This is the main m-file and likely the only one you will have to worry about. It contains a big for loop which takes the initial conditions for the ball's flight and calculates one bar impact, storing the data in the matrix 'P'. The post-impact conditions then become the new initial conditions. It loops as many times as indicated.
• binSrch - Uses a binary search method to locate the time where in ball intersects the bar, based off of the initial flight conditions and parameters. It returns the time of intersection (denoted 't2').
• checkLocking - Determines whether or not the ball is locking. Locking is a phenomenon in which the ball's velocity decays to zero, undergoing an infinite number of bounces in the absorbing region of the bar's motion. If the flight time is less than an arbitrarily small value, the ball is determined to be locking, and a value of 1 is returned.
• impact - This function takes the initial conditions and time of impact as inputs. It uses a simple impact model to calculate the post-impact positions and velocities of the ball.
• calculateLaunch - Determines whether or not the ball will be relaunched after locking. If the motion of the bar, and the position of the ball are such that the vertical acceleration of the bar will exceed gravity at some point during its periodic motion, then the ball will be relaunched. Otherwise, the ball will never be relaunched, and the simulation will terminate.
• plotTraj - This function is used only to plot the trajectories of the ball and the bar. This is only used as a visual aid and is helpful for debugging. It can easily be turned off to speed up the simulation.

Explanation of Important Inputs & Parameters

First, open the bBallSim m-file. The first few lines will look like this:

function [P, N] = bBallSim(A_x, A_z, A_th, p)

% SYSTEM PARAMETERS
num_impacts = 500;    % Number of impacts simulator will calculate before terminating

A = [A_x; A_z; A_th];    % Position amplitude of bar, nondimensional [A_x, A_z, A_th]
phi = [pi/2; pi/2; p];    % Phase angle of bar [phi_x, phi_z, phi_th]
f = [1; 2; 1];    % Frequencies of bar motions [f_x, f_z, f_th]
w = 2*pi.*f;    % [w_x, w_z, w_th]

There are four important inputs for this version of the program.

• A_x is the nondimensionalized position amplitude of the bar in the x (horizontal) direction.
• A_z is the nondimensionalized position amplitude of the bar in the z (vertical) direction.
• A_th is the amplitude in the theta direction (angular about the y). It is already dimensionless.
• p is the relative phase between the theta motion and the other motions.

Nondimensionalizations are as follows:

Position: $p'=p*(f(1)^{2}/g)\,$ where f(1) is equal to the first frequency in the vector f (or the horizontal frequency) and g is equal to the acceleration due to gravity

Velocity: $v'=v*(f(1)/g)\,$

Acceleration: $a'=a/g\,$

Simple Test

For example, if one were to input the following:

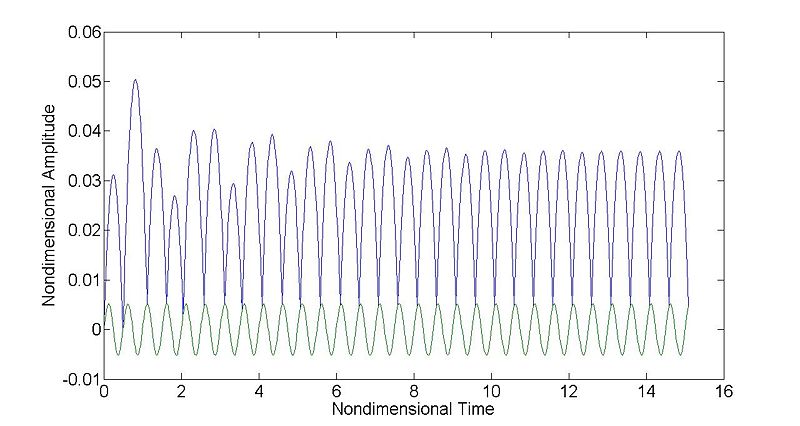
[P, N] = bBallSim(0, 0.0052, 0, 0);

This is setting a motion with zero amplitude in the x and theta directions. 0.0052 is the nondimensional equivalent of 8m/s^2 in the z direction. If this simulation is run for 100 impacts with e = [0.8 0.8], the following plot will be created:

399 Write-up and Raw Data

The following is a 399 Write-up from a 2009-2010 independent study conducted by Undergraduate Eric Bell. The paper uses data from both physical experimentation as well as the simulator described above.