Passive Filters

RL Circuits

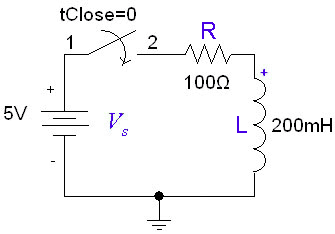
Charging

If the inductor is initially uncharged and we want to charge it by inserting a voltage source $V_s$ in the RL circuit:

The inductor initially has a very high resistance, as energy is going into building up a magnetic field. Once the magnetic field is up and no longer changing, the inductor will act like a short circuit. The current at steady state will be equal to $I_0=V_s/R$. Since the inductor is acting like a short circuit at steady state, the voltage across the inductor then will be 0. The current through the inductor is given by:

$i_L(t)=I_0(1-e^{-\frac{R}{L}t})$

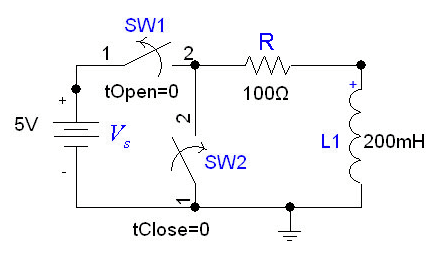
Discharging

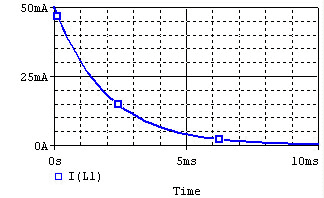
In the following circuit, the inductor initially has current $I_0=V_s/R$ flowing through it; we replace the voltage source with a short circuit at $t=0$.

After we cut out the voltage source, the voltage across the inductor will be $I_0*R$, but the higher voltage will be at the negative terminal of the inductor. Thus, $I_0=-V/R$. The the current flowing through the inductor at time t is given by:

$i_L(t)=I_0{e}^{-\frac{R}{L}t}$

where $I_0=-V_s/R$.

The time constant for the RL circuit is equal to $L/R$.

The voltage and current of the inductor for the circuits above are given by the graphs below, from t=0 to t=5L/R. The voltage is measured at the "+" terminal of the inductor, relative to the ground. A positive current flows into the inductor from this terminal; a negative current flows out of this terminal.:

Inductor

	Voltage	Current
Charge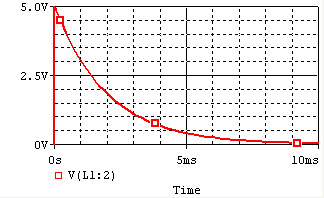
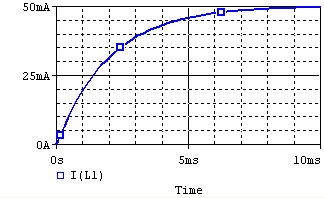
Discharge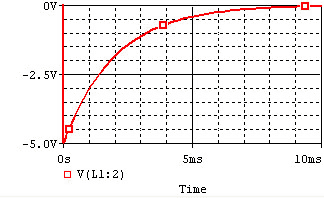

Remember that for an inductor, $v(t)=L*di/dt$. Note that the voltage across the inductor can change instantly at t=0, but the current changes slowly.