Design and Control of a Pantograph Robot
Overview
The goal of this project was to design and build a 2-DOF Pantograph Robot. The user would be able to specify and X and Y location for the end point of the pantograph, along with different paths that the robot arm could take. The basic circuit design and computer code was taken from the High Speed Motor Control project and adapted to work with our robot design.
Kinematics
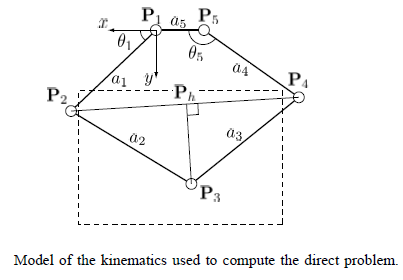
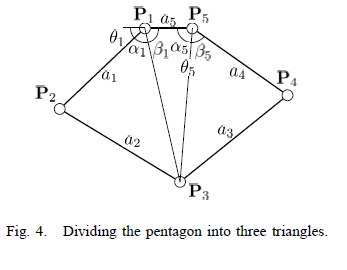
The kinematics for our robot design were derived from The Pantograph Mk. II - A Haptic Instrument. The forward and inverse kinematics as used in the MATLAB program are shown below, along with diagrams from the paper showing how the reference frames are defined in our setup. These angles are all calculated in radians, other parts of the programs convert this to degrees for graphing and user interfaces. The full programs can be found in the zip files below.
Forward Kinematics
x2 = L1 * cos(theta); y2 = L1 * sin(theta); y4 = L4 * sin(alpha); x4 = L4 * cos(alpha) - L5; two_to_four = sqrt((x2-x4).^2 + (y2-y4).^2); two_to_h = (L2^2 - L3^2 + two_to_four.^2) ./ (2 * two_to_four); yh = y2 + (two_to_h./two_to_four).*(y4-y2); xh = x2 + (two_to_h./two_to_four).*(x4-x2); three_to_h = sqrt(L2^2 - two_to_h.^2); x3 = xh + (three_to_h./two_to_four) .* (y4-y2); y3 = yh - (three_to_h./two_to_four) .* (x4-x2);
Inverse Kinematics
L13 = sqrt(x3.^2+y3.^2); L53 = sqrt((x3+L5).^2 + y3.^2); alphaOne = acos((L1.^2 + L13.^2 - L2.^2)./(2.*L1.*L13)); betaOne = atan2(y3,-x3); thetaOne = pi - alphaOne - betaOne; alphaFive = atan2(y3,x3+L5); betaFive = acos((L53.^2 + L4.^2 - L3.^2)./(2.*L53.*L4)); thetaFive = alphaFive + betaFive;