Difference between revisions of "Passive Filters"
| Line 1: | Line 1: | ||
__TOC__ |
|||
==RL Circuits== |
|||
We can build some very simple filters out of a capacitor and a resistor. A filter will block some frequencies, while admitting others. |
|||
===Charging=== |
|||
If the inductor is initially uncharged and we want to charge it by inserting a voltage source <math>V_s</math> in the RL circuit: |
|||
Better filters can be made out of op-amps. |
|||
| ⚫ | |||
==Low-Pass Filters (LPF)== |
|||
The inductor initially has a very high resistance, as energy is going into building up a magnetic field. Once the magnetic field is up and no longer changing, the inductor will act like a short circuit. The current at steady state will be equal to <math>I_0=V_s/R</math>. Since the inductor is acting like a short circuit at steady state, the voltage across the inductor then will be 0. The current through the inductor is given by: |
|||
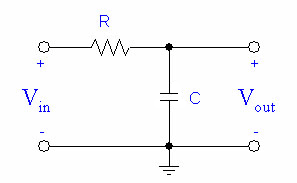
A low pass filter will admit lower frequencies and block out high ones. This can help us smooth out our signals and get rid of high frequency noise. |
|||
We can make one by hooking up our capacitor and resistor like this: |
|||
<math>i_L(t)=I_0(1-e^{-\frac{R}{L}t})</math> |
|||
| ⚫ | |||
When set R=500Ω and C=2nF, and hook up an AC voltage source, the voltage we see at <math>V_out</math> depends on the frequency of our source. Here is a plot of the frequency response of the filter, on a logarithmic scale from 10Hz to 10MHz: |
|||
===Discharging=== |
|||
In the following circuit, the inductor initially has current <math>I_0=V_s/R</math> flowing through it; we replace the voltage source with a short circuit at <math>t=0</math>. |
|||
[[Image: |
[[Image:RC_LPF_frequncy_response.gif]] |
||
As we can see, the filter blocks the higher frequncies. |
|||
After we cut out the voltage source, the voltage across the inductor will be <math>I_0*R</math>, but the higher voltage will be at the negative terminal of the inductor. Thus, <math>I_0=-V/R</math>. The the current flowing through the inductor at time ''t'' is given by: |
|||
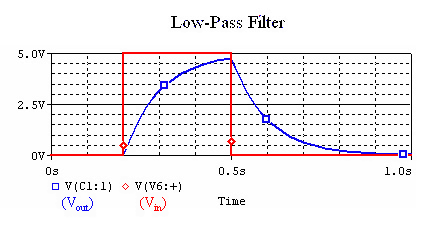
Since a square wave is made out of a superposition of many sine waves, the low-pass filter will block the sine waves with higher frequencies. Our input and output will look like: |
|||
<math>i_L(t)=I_0e^{-\frac{R}{L}t}</math> |
|||
[[Image:RC_LPF_square_wave.gif]](C=200uF, R=500Ω) |
|||
where <math>I_0=-V_s/R</math>. |
|||
==High-Pass Filter (HPF)== |
|||
The ''time constant'' for the RL circuit is equal to <math>L/R</math>. |
|||
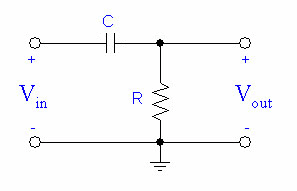
A high pass filter will block out lower frequencies while letting high frequencies through. The output will respond more strongly to changes in the input signal, such as that coming from a motion detector. |
|||
We can make a simple high-pass filter by hooking up our capacitor and resistor like this: |
|||
The voltage and current of the inductor for the circuits above are given by the graphs below, from ''t=0'' to ''t=5L/R''. The voltage is measured at the "+" terminal of the inductor, relative to the ground. A positive current flows into the inductor from this terminal; a negative current flows out of this terminal.: |
|||
[[Image:RC_HPF_schematic.gif]] |
|||
{| border="1" cellspacing="0" cellpadding="5" align="center" |
|||
|+'''Inductor''' |
|||
|- |
|||
! !!Voltage !! Current |
|||
|- |
|||
!Charge !! [[Image:RL_charge_voltage.gif]] || [[Image:RL_charge_current.gif]] |
|||
|- |
|||
!Discharge !! [[Image:RL_discharge_voltage.gif]] || [[Image:RL_discharge_current.gif]] |
|||
|- |
|||
|} |
|||
The frequncy response of a filter with R=500Ω and C=2nF looks like this: |
|||
Remember that for an inductor, <math>v(t)=L*di/dt</math>. Note that the voltage across the inductor can change instantly at ''t=0'', but the current changes slowly. |
|||
[[Image:RC_HPF_frequency_Response.gif]] |
|||
This time, the filter blocks the lower frequencies. |
|||
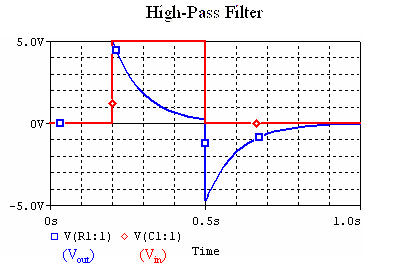
When we put a square wave though the filter, the resulting waveform looks like this: |
|||
[[Image:RC_HPF_square_wave.gif]](C=200uF, R=500Ω) |
|||
Notice that when the input voltage drops to zero, the output voltage becomes negative. This is because the capacitor is discharging, and forcing the current backwards. |
|||
Revision as of 16:08, 20 June 2006
We can build some very simple filters out of a capacitor and a resistor. A filter will block some frequencies, while admitting others.
Better filters can be made out of op-amps.
Low-Pass Filters (LPF)
A low pass filter will admit lower frequencies and block out high ones. This can help us smooth out our signals and get rid of high frequency noise.
We can make one by hooking up our capacitor and resistor like this:
When set R=500Ω and C=2nF, and hook up an AC voltage source, the voltage we see at depends on the frequency of our source. Here is a plot of the frequency response of the filter, on a logarithmic scale from 10Hz to 10MHz:
File:RC LPF frequncy response.gif
As we can see, the filter blocks the higher frequncies.
Since a square wave is made out of a superposition of many sine waves, the low-pass filter will block the sine waves with higher frequencies. Our input and output will look like:
High-Pass Filter (HPF)
A high pass filter will block out lower frequencies while letting high frequencies through. The output will respond more strongly to changes in the input signal, such as that coming from a motion detector.
We can make a simple high-pass filter by hooking up our capacitor and resistor like this:
The frequncy response of a filter with R=500Ω and C=2nF looks like this:
File:RC HPF frequency Response.gif
This time, the filter blocks the lower frequencies.
When we put a square wave though the filter, the resulting waveform looks like this:
Notice that when the input voltage drops to zero, the output voltage becomes negative. This is because the capacitor is discharging, and forcing the current backwards.