The sandbox

test

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-3dB point) = \frac{1}{2\pi}(R1*R2*C1*C2)^\frac{1}{2} }

$x[n+1]=x[n]+\gamma (u[n]-x[n])-K_{P}\sum _{j=1}^{N}({\frac {1}{N}}x_{j}[n])+K_{I}\sum _{j=1}^{N}({\frac {1}{N}}w_{j}[n])$

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w[n+1] = w[n] - K_I\sum_{j=1}^N(\frac{1}{N}x_j[n]) }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} \dot u_x \\ \dot u_y \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 2(R_x-x_{Mx}) & (R_y-x_{My}) & 0 \\ 0 & 1 & 0 & (R_x-x_{Mx}) & 2(R_y-x_{My})\\ \end{bmatrix} \begin{bmatrix} k_{Mx} & 0 & 0 & 0 & 0 \\ 0 & k_{My} & 0 & 0 & 0 \\ 0 & 0 & k_{Mxx} & 0 & 0 \\ 0 & 0 & 0 & k_{Myy} & 0 \\ 0 & 0 & 0 & 0 & k_{Mxy} \\ \end{bmatrix} \begin{bmatrix} g_{Mx}-x_{Mx} \\ g_{My}-x_{My}\\ g_{Mxx}-x_{Mxx} \\ g_{Myy}-x_{Myy} \\ g_{Mxy}-x_{Mxy} \\ \end{bmatrix} }

Spur Gears

	125px

Rack and Pinion

Bevel Gears

Helical Gears

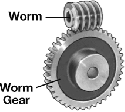
Worm Drives

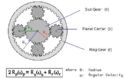
Planetary Gears

Ball Screw

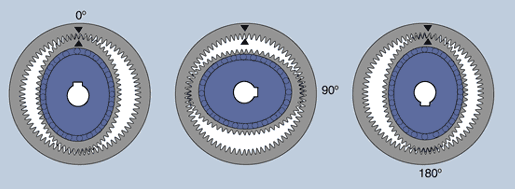
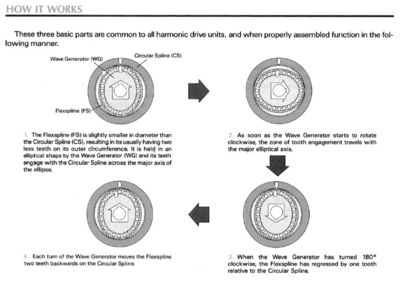
Harmonic Drive Gears

400px