High Speed Vision System and Object Tracking

Last modified 6 June, 2009

Calibrating the High Speed Camera

Figure 1: Calibration grid with distortion.

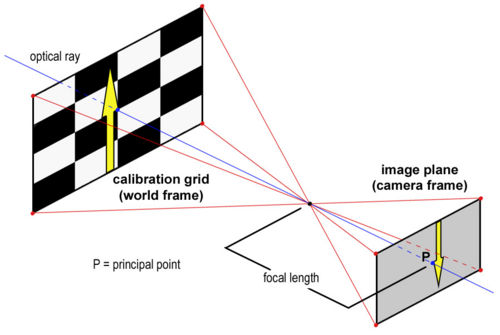
Before data can be collected from the HSV system, it is critical that the high speed camera be properly calibrated. In order to obtain accurate data, there is a series of intrinsic and extrinsic parameters that need to be taken into account. Intrinsic parameters include image distortion due to the camera itself, as shown in Figure 1. Extrinsic parameters account for any factors that are external to the camera. These include the orientation of the camera relative to the calibration grid as well as any scalar and translational factors.

In order to calibrate the camera, download the Camera Calibration Toolbox for Matlab. This resource includes detailed descriptions of how to use the various features of the toolbox as well as descriptions of the calibration parameters.

For Tracking Objects in 2D

To calibrate the camera to track objects in a plane, first create a calibration grid. The Calibration Toolbox includes a calibration template of black and white squares of side length = 3cm. Print it off and mount it on a sheet of aluminum or PVC to create a stiff backing. This grid must be as flat and uniform as possible in order to obtain an accurate calibration.

Intrinsic Parameters

Following the model of the first calibration example on the Calibration Toolbox website, use the high speed camera to capture 10-20 images, holding the calibration grid at various orientations relative to the camera. 1024x1024 images can be obtained using the "Moments" program. The source code can be checked out here.

Figure 2: Calibration grid undistorted.

Calibration Tips:

• One of the images must have the calibration grid in the tracking plane. This image is necessary for calculating the extrinsic parameters and will also be used for defining your origin.
• The images must be saved in the same directory as the Calibration Toolbox.
• Images must be saved under the same name, followed by the image number. (image1.jpg, image2.jpg...)
• The first calibration example on the Calibration Toolbox website uses 20 images to calibrate the camera. I have been using 12-15 images because sometimes the program is incapable of optimizing the calibration parameters if there are too many constraints.

The Calibration Toolbox can also be use to compute the undistorted images as shown in Figure 2.

After entering all the calibration images, the Calibration Toolbox will calculate the intrinsic parameters, including focal length, principal point, and undistortion coefficients. There is a complete description of the calibration parameters here.

Extrinsic Parameters

In addition, the Toolbox will calculate rotation matrices for each image (saved as Rc_1, Rc_2...). These matrices reflect the orientation of the camera relative to the calibration grid for each image.

Figure 3: Projection of calibration grid onto the image plane.

Figure 3 is an illustration of the pinhole camera model that is used for camera calibration. Since the coordinates of an object captured by the camera are reported in terms of pixels (camera frame), these data have to be converted to metric units (world frame).

In order to solve for the extrinsic parameters, first use the 'normalize' function provided by the calibration toolbox:

  [xn] = normalize(x_1, fc, cc, kc, alpha_c);

where x_1 is a matrix containing the coordinates of the extracted grid corners in pixels for image1. The normalize function will apply any intrinsic parameters and return the (x,y) point coordinates free of lens distortion. These points will be dimensionless as they will all be divided by the focal length of the camera. Next, change the [2xn] matrix of points in (x,y) to a [3xn] matrix of points in (x,y,z) by adding a row of all ones. xn should now look something like this:

$\mathbf {xn} ={\begin{bmatrix}x_{c}1/z_{c}&x_{c}2/z_{c}&...&x_{c}n/z_{c}\\y_{c}1/z_{c}&y_{c}2/z_{c}&...&y_{c}n/z_{c}\\z_{c}/z_{c}&z_{c}/z_{c}&...&z_{c}/z_{c}\end{bmatrix}}$ Where x_c, y_c, z_c, denote coordinates in the camera frame. z_c = focal length of the camera as calculated by the Calibration Toolbox.

Then, apply the rotation matrix, Rc_1:

  [xn] = Rc_1*x_n;

We now have a matrix of dimensionless coordinates describing the location of the grid corners after accounting for distortion and camera orientation. What remains is to apply scalar and translational factors to convert these coordinates to the world frame. To do so, we have the following equations:

$X_{1}(1,1)=S1*xn(1,1)+T1\,$

$X_{1}(2,1)=S2*xn(2,1)+T2\,$

Where:

$S=(focallength)*(numberofmillimeters/pixel)\,$

X_1 is the matrix containing the real world coordinates of the grid corners and is provided by the Calibration Toolbox. Cast these equations into a matrix equation of the form:

$Ax=b\,$

Where:

$\mathbf {A} ={\begin{bmatrix}xn(1,1)&1&0&0\\0&0&xn(2,1)&1\\xn(1,2)&1&0&0\\0&0&xn(2,2)&1\\.&.&.&.\\.&.&.&.\\.&.&.&.\\xn(1,n)&1&0&0\\0&0&xn(2,n)&1\end{bmatrix}}$ $\mathbf {x} ={\begin{bmatrix}S_{1}\\T_{1}\\S_{2}\\T_{2}\end{bmatrix}}$ $\mathbf {b} ={\begin{bmatrix}X_{1}(1,1)\\X_{1}(2,1)\\X_{1}(1,2)\\X_{1}(2,2)\\.\\.\\.\\X_{1}(2,n)\\X_{1}(2,n)\end{bmatrix}}$

Finally, use the Matlab backslash command to compute the least squares approximation for the parameters S1, S2, T1, T1:

  x = A\b

Now that all the parameters have been calculated, percentage error can be calculated, by applying the entire transformation process to the x_1 matrix and comparing the results to the X_1 matrix. If carefully executed, this calibration method can yield percent errors as low as 0.01%.

For Tracking Objects in 3D

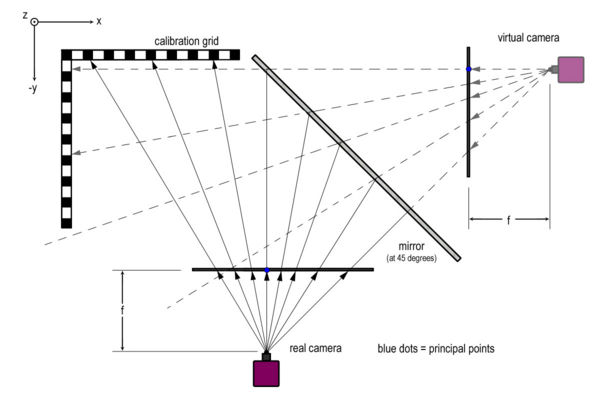
In order to obtain the coordinates of an object in three dimensions, a mirror can be used in order to create a "virtual camera," as shown in Figure 4.

Figure 4: Three dimensional imaging with mirror at 45 degrees.

Calibrating the camera to work in three dimensions is very similar to the two dimensional calibration. The main difference is the calibration grid itself. Instead of using a single flat plane for the calibration grid, an additional grid has to be constructed, consisting of two planes at 90 degrees as shown in the figure. This grid must be visible by both the "real" and "virtual" cameras. The purpose of this is to create a common origin. Having a common origin for both cameras will become critical in calculating an object's position in three dimensions.

Follow the steps for the 2D calibration and complete a separate calibration for each camera. The two sets of intrinsic parameters that are obtained should be identical in theory. In practice, they are likely to differ slightly.

Once the real world coordinates of an object in the XZ and YZ planes are obtained, the 3D position of the object still has to be obtained. The raw data is inaccurate because it represents the projection of the object's position onto the calibration plane. For the methodology and code required to execute these calculations, refer to the section entitled "Calculating the Position of an Object in 3D."

Post-Processing of Data

Calculating the Position of an Object in 3D

By comparing the data captured by the "real" camera and the "virtual" camera, it is possible to triangulate the three dimensional position of an object. The calibration procedures discussed earlier provide the real world (x,y) coordinates of any object, projected onto the calibration plane. By determining the fixed location of the two cameras, it is possible to calculate two position vectors and then compute a least squares approximation for their intersection.

The Calibration Toolbox provides the principal point for each camera measured in pixels. The principal point is defined as the (x,y) position where the principal ray (or optical ray) intersects the image plane. This location is marked by a blue dot in Figure 4. The principal point can be converted to metric by applying the intrinsic and extrinsic parameters discussed in the section "Calibrating the High Speed Camera."

From here, the distance from the cameras to the origin can be determined from the relationship:

$distance=(focallength)*(numberofmillimeters/pixel)\,$

Once this distance is calculated, the parallel equations can be obtained for a line in 3D with 2 known points:

$(x-x_{1})/(x_{2}-x_{1})=(y-y_{1})/(y_{2}-y_{1})=(z-z_{1})/(z_{2}-z_{1})\,$

Which can be rearranged in order to obtain 3 relationships:

$x*(y_{2}-y_{1})+y*(x_{1}-x_{2})=x_{1}*(y_{2}-y_{1})+y_{1}*(x_{1}-x_{2})\,$

$x*(z_{2}-z_{1})+z*(x_{1}-x_{2})=x_{1}*(z_{2}-z_{1})+z_{1}*(x_{1}-x_{2})\,$

$y*(z_{2}-z_{1})+z*(y_{1}-y_{2})=y_{1}*(z_{2}-z_{1})+y_{1}*(y_{1}-y_{2})\,$

These equations can be cast into matrix form:

$\mathbf {A} ={\begin{bmatrix}y_{2}-y_{1}&x_{1}-x_{2}&0\\z_{2}-z_{1}&0&x_{1}-x_{2}\\0&z_{2}-z_{1}&y_{1}-y_{2}\end{bmatrix}}$

$\mathbf {x} ={\begin{bmatrix}x\\y\\z\end{bmatrix}}$ $\mathbf {b} ={\begin{bmatrix}x_{1}*(y_{2}-y_{1})+y_{1}*(x_{1}-x_{2})\\x_{1}*(z_{2}-z_{1})+z_{1}*(x_{1}-x_{2})\\y_{1}*(z_{2}-z_{1})+y_{1}*(y_{1}-y_{2})\end{bmatrix}}$

There should be one set of equations for each vector, for a total of six equations. A should be a [6x3] matrix, and b should be a vector of length 6. Computing A\b in Matlab will yield the least squares approximation for the intersection of the two vectors.