Difference between revisions of "Optical Locating"
| Line 51: | Line 51: | ||
<math>\frac{1}{T} \int_{0}^{T}f_1\times f_2\, dt</math> |
<math>\frac{1}{T} \int_{0}^{T}f_1\times f_2\, dt</math> |
||
<math>=\frac{1}{T} \int_{0}^{T}-\frac{AB}{2} \times \{ cos[(\omega_1 + \omega_2 )t+\phi ]-cos[(\omega_1 - \omega_2 )t-\phi ]\} \, dt</math> |
<math>=\frac{1}{T} \int_{0}^{T}-\frac{AB}{2} \times \{ cos[(\omega_1 + \omega_2 )t+\phi ]-cos[(\omega_1 - \omega_2 )t-\phi ]\} \, dt</math> |
||
<math>= -\frac{AB}{2T} \int_{0}^{T} cos[(\omega_1 + \omega_2 )t+\phi ] \,dt +</math> |
|||
= -0.5AB/TINT(0, T) {cos[(1 + 2) t + ] - cos[(1 - 2) t - ]}dt |
|||
=-0.5AB/TINT(0, T) cos[(1 + 2) t + ]dt + 0.5AB/TINT(0, T) cos[(1 - 2) t - ]dt |
=-0.5AB/TINT(0, T) cos[(1 + 2) t + ]dt + 0.5AB/TINT(0, T) cos[(1 - 2) t - ]dt |
||
When T , the first part 0, and the second part 0.5AB, when and only when 1 = 2 and = 0. |
When T , the first part 0, and the second part 0.5AB, when and only when 1 = 2 and = 0. |
||
Revision as of 17:21, 11 December 2008
Overview
Many tracking applications require that the system identify the location of information within a visual field. This could be seeking a color, or a shape, or just the centroid of light intensity. This page discusses the use of a duo-lateral photodiode to sense the centroid of light within its field of view. The documented method uses a passive retro-reflective target and optics.
System Design
The system is designed to obtain the location of a reflective target within its visual field and track it at high speeds. Figure 1 is a system diagram showing the functional blocks of the system. The system needs to be able to obtain the position of the target relative to the current direction the "eye" is facing, which requires that it be able to distinguish between the target signal and potential ambient light, and then produce a signal which the microcontroller can utillize to drive motors which orient the eye toward the target.
The system contains the following elements:
- Eye structure on a 2-DoF gimbal
- Position-sensing detector
- Target illumination circuit
- Optics
- Phase-sensitive detection circuit
- Microcontroller
Position-Sensing Detector
The position sensing detector used in this system is a DLS-4, a two-dimensional lateral-effect position-sensing device from OSI Optoelectronics. This sensor (as shown in the image at right) has a 4mm x 4mm sensing area and has four output leads, one pair for each axis of measurement. Each output lead acts as a current source (due to photoelectric effect) either sourcing or sinking current based on the intensity of the light it is receiving and the distance from the centroid of the light spot from the terminal corresponding to the lead. One pair of leads corresponding to a direction pair (left-right or up-down) will be sourcing current while the other sinks current. For further details see the lateral-effect photodiode.
Target Illumination
Illuminating the target was achieved via eight TSHF 5210 infrared-emitting diodes (IRED's)(http://www.vishay.com/docs/81303/tshf5410.pdf). These were arranged into two parallel groups of four which were each soldered together as part of the "eye"structure. The IRED illumination circuit was pulsed synchronously with the phase-sensitive detector switch at 20 kHz. The target was a 1.5" diameter sphere covered with retroreflective tape, providing a decent brightness spot even at distances beyond one meter.
Optics
If light is directed at the sensor in a parallel beam (such as from a flashlight or laser, or potentially the reflection from a distant target), the light available from the field of view can be overshadowed by the intensity of the light in the beam, resulting in uniform distribution of the light on the sensing surface until the light source becomes occluded by the edge of the case or structure, resulting in a shadow. In theory, if the beam were narrow with respect to the size of the sensing area, the placement of the beam on the sensing area should produce output currents which are representative of the proximity of the "dot" to each edge of the sensor. The sensing area is only 4mm square, and even the "dot" produced by a laser pointer is 2mm in diameter with additional scatter, so the dot is anything but "small". To reduce this "large-dot" problem, an optical lens (salvaged from a laser pointer) and infrared filter (http://www.edmundoptics.com/onlinecatalog/displayproduct.cfm?productID=1918) were used.
Phase-Sensitive Detection Circuit
The difficulty in trying to identify a target which could be buried within background ambient light is differentiating between the ambient signal and the target signal. The method of achieving that separation that this system uses is called phase-sensitive-detection. Essentially, the circuit uses an active low-pass filter to compare the centroid of light with the illumination on to the centroid of light with the illumination off, by switching from one lead when the illumination is on to the other when it is off. The use of the other lead when the illumination is off allows the filter to compare
Overview
One effective way to recover the small signal buried by large ambient noise is to use the so called phase sensitive detector, or lock-in amplifier. A phase sensitive detector achieves narrow bandwidth amplification by reducing the noise content at falling outside the interested bandwidth.
When the noise is white in nature, we can reduce its level of magnitude dramatically by limiting the bandwidth of detection, which includes the frequency occurring to the signal while excludes the frequencies occurring to the noise. Phase sensitive detection enables extremely narrow bandwidth detection (0.001Hz is normal). Typical application scenario is using electric transducers where the amplitude of noise is in mili volts and the signal falls into nano volt region. Sophisticated phase sensitive detector can extract signals buried in noise that is 107 times larger in magnitude.
In this article, we focus on a quick and easy method of building a phase sensitive detector from op-amps and analog switches.
Mathematical model
Consider two signals, and , where ,
Then, the product of and is:
Let’s integrate the product over time [0, T):
= -0.5AB/TINT(0, T) {cos[(1 + 2) t + ] - cos[(1 - 2) t - ]}dt =-0.5AB/TINT(0, T) cos[(1 + 2) t + ]dt + 0.5AB/TINT(0, T) cos[(1 - 2) t - ]dt When T , the first part 0, and the second part 0.5AB, when and only when 1 = 2 and = 0.
This is the mathematical foundation of phase sensitive detection, because all signals can be broken down in to several harmonic components. And by intentionally modulating the useful signal and do the maths, we can recover the signal from the noise.
(I'll re-type it later using mathtype)
Method
A phase sensitive detection can be split into 6 stages:
1. Modulation: Modulate the signal at a certain frequency.
2. Pre-amplification: A high-speed amplifier required to amplify the signal (along with the noise) to a suitable level for succeeding circuit. We can also stick in a high pass filter (can be a capacitor) after amplification, just to eliminate the DC portion of the noise.
3. Reference circuit: Usually a pulse wave at the modulating frequency, which can be from a function generator, or a 555 timer, or PIC, etc.
4. Multiplier: At this stage, we multiply the pre-amplified signal (along with the noise) with the reference signal. One easy way to do multiplication is suggested here: we use the reference signal to turn on and off an analog switch periodically, and let the modulated input signal pass the analog switch. So when the switch is ON (meaning connected), the output is ‘input 1’, and when the switch is OFF (meaning disconnected), the output is ‘input 0’.
5. Integrator (demodulation): Let the multiplied signal pass through an integrator. The multiplied signal can have a lot of components – almost all of them will become zero after integration (see explanation in the mathematical model), but the one which is the product of the modulated signal and the reference signal will remain, because they are at the same frequency and the same phase angle. This is the essence of phase sensitive detection – only the product of the two signals that are ‘in phase’ will remain after integration. ‘In phase’ means the two signals share common frequency and phase angle. We can also do amplification at the integration stage by sticking in a feedback resistor (see the example circuit diagram), just for convenience.
6. Low pass filter: After integration, the signal is recovered and demodulated to a DC output. However, it may not be a perfect DC voltage due to high frequency spikes that still exist. That’s why the low pass filter come into play.
Example circuit diagram
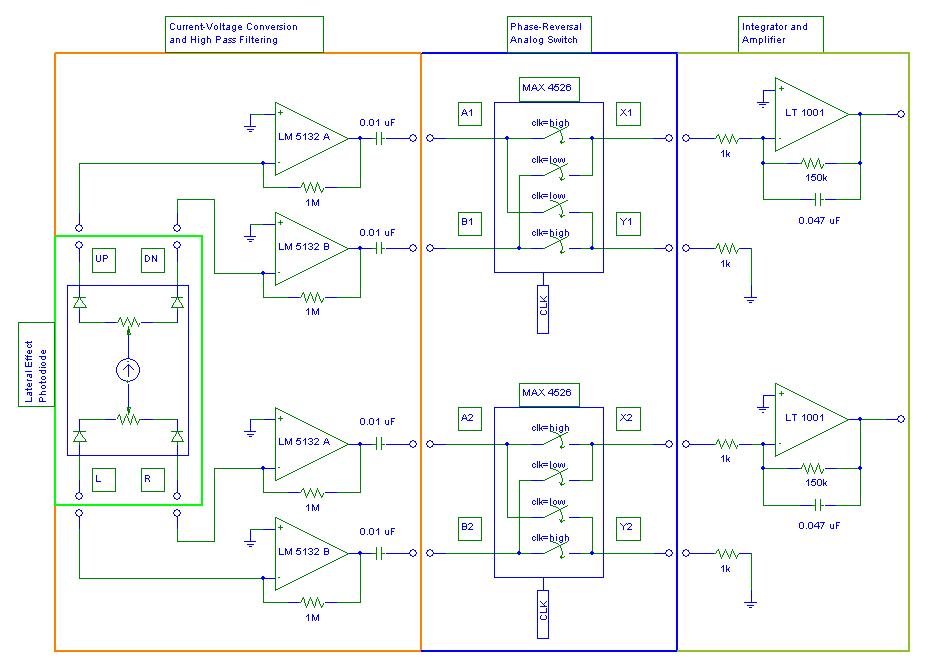
The concept of phase sensitive detection has been proved effective in optical tracking with lateral effect photodiode. The following circuit picks up the difference of the two corresponding output pins of the photodiode, in order to tell the position of the centroid of IR light on the photodiode sensing surface. The connection for the Y+ and Y- pins of the photodiode is exactly the same with what’s shown here for X+ and X-. The timer is realized by a 555 chip, and the chip for analog switch is Maxim 4056.
Commercial phase sensitive detectors
This link below provides some useful information on commercially available phase sensitive detectors, or lock-in amplifiers.
[1]SRS series Lock-in amplifiers





![{\displaystyle =-{\frac {AB}{2}}\times {cos[(\omega _{1}+\omega _{2})t+\phi ]-cos[(\omega _{1}-\omega _{2})t-\phi ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c16297ab472330e232f91edb45dca34472d795ed)

![{\displaystyle ={\frac {1}{T}}\int _{0}^{T}-{\frac {AB}{2}}\times \{cos[(\omega _{1}+\omega _{2})t+\phi ]-cos[(\omega _{1}-\omega _{2})t-\phi ]\}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/085897a67476129152d5f7e97a0b407ce529b205)
![{\displaystyle =-{\frac {AB}{2T}}\int _{0}^{T}cos[(\omega _{1}+\omega _{2})t+\phi ]\,dt+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb249227bdff05626259cbe84d73be81097d754)