Indoor Localization System

Motivation

For relatively simple autonomous robots, knowing an absolute position in the world frame is a very complex challenge. Many systems attempt to approximate this positioning information using relative measurements from encoders, or local landmarks. Opposed to an absolute system, these relativistic designs are subject to cumulating errors. In this design, the positioning information is calculated by an external computer which then transmits data over a wireless module.

This system can be envisioned as an indoor GPS, where positioning information of known patterns is transmitted over a wireless module available for anyone to read. Unlike a GPS, this vision system has much higher resolution and is designed for indoor use.

Overview of Design

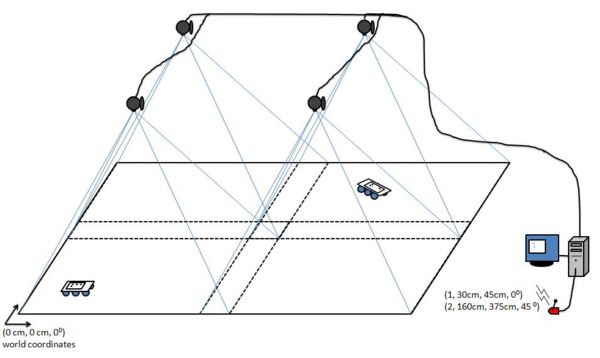
This system uses four standard webcams to locate known patterns in a real time image, and transmit positioning information over a serial interface. This serial interface is most often connected to a wireless Zigbee® module. The cameras are mounted in fixed positions above the target area. The height of the cameras can be adjusted to increase either the positioning resolution or the area of the world frame. These constraints are a function of the field of view of the lenses. Below is a diagram illustrating this system’s basic setup.

Overview of System

Here, we can see the four cameras are mounted rigidly above the world frame. Note that the cameras actual placement must have an overlap along inside edges at least the size of one target. This is necessary to ensure any given target is at least fully inside one camera’s frame.

Goals

• To provide real-time (X, Y, θ) position information to an arbitrary number of targets (<20) in a fixed world frame using a home-made computer vision system.

• Maximize throughput and accuracy

• Minimize latency and noise

• Easy re-calibration of camera poses.

• Reduced cost (as compared to real-time operating systems and frame grabbing technology)

Tools Used

Software

• IDE: Microsoft Visual C++ Express Edition – freeware (http://www.microsoft.com/express/default.aspx)

• Vision Library: Intel OpenCV – open source c++ (http://sourceforge.net/projects/opencvlibrary/)

• Camera Capture Library: VideoInput – open source c++ (http://muonics.net/school/spring05/videoInput/)

Hardware

• Four Logitech QuickCam Communicate Deluxe USB2.0 webcams

• One 4-port USB2.0 Hub

• Computer to run algorithm

Algorithm Design

Overview

To identify different objects and transmit position and rotation information a 3x3 pattern of black circles is used. To create both position and orientation, the patterns must have at least 3 dots in a rotationally invariant configuration.

Pre-Processing

Target Classification

Before the system is executed in real time, two tasks must be completed. The first is pre-processing the possible targets to match (the patterns of 3x3 dots). This is done by first creating a subset of targets from the master template. Each target must be invariant in rotation, reflection, scale and translation. A set of targets has been included in the final project, with sample patterns. When the program is executed in real time, it will only identify targets from the trained subset of patterns.

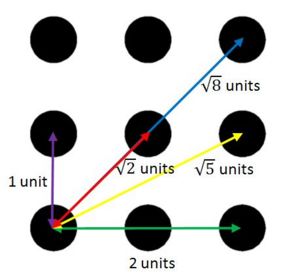
When the targets are pre-processed, unique information is recorded to identify each pattern. In particular, the algorithm counts the number of dots and the relative spacing between each dot. In this sense, the pattern is identified as a unique number (corresponding to the order of target patterns in the image directory), the number of dots in the pattern, and the normalized spacing between each dot. Since the pattern is a fixed 3x3 grid, the only possible spacing between dots is 1, √2, 2, √5, or √8 units. As in networking theory, this is a fully connected network and thus has at most n*(n-1)/2 links. Since the most number of dots in a pattern is 9, the maximum number of interspacing distances is 9*8/2 = 36.

The last piece of information recorded is the orientation of the target. Below is a picture of this configuration. *Note to change the target, various dots are removed.

Pattern Recognition

Camera Calibration

The second required step before the system can be used is training the cameras both their intrinsic parameters (focal length, geometric distortions, pixel to plane transformation) and their extrinsic pose parameters (rotation and translation of origins). In other words, the pixels in the image must be correlated to the world frame in centimeters or inches. This step is performed by using a simple linear least squares best fit model. The calibration process needs at least 6 points as measured in the world and image frames to compute a 3x4 projection matrix. In practice, we use more than these 6 points to add redundancy and help best compute an accurate projection matrix. The method used is outlined in Multiple View Geometry in Computer Vision by Richard Harley and Andrew Zisserman.

Real Time Operation

In the actual operation of the program, it flows in an infinite loop performing three basic tasks. As soon as a new frame is available, the program follows the following outlined steps.

Image Formation

First, the computer converts the image to a grayscale (0-255) image. After this operation is performed, the algorithm thresholds the image based on a set level. This converts the grayscale image to a binary image by converting colors above the threshold to white (255) and all other values to black (0). After these two operations are performed, the resultant image is a black and white binary image. The default threshold level is set to 80.

Pattern Isolation

After the image has been prepared in the binary format, all the contours must be outlined. This process is known as connected-component-labeling (CCL) in computer vision. This process identifies continuous “blobs” or regions of pixels that are adjacent. In OpenCV the connected components are stored into a linked list data structure called a contour. Fortunately, the connected component labeling process is a native function of OpenCV and we only have to process the resultant contour data structure. To do this, the program iterates through each contour in the data structure, extracting position and area information (in pixels). This data is stored into a custom data structure called dotData. While processing each contour, the algorithm groups the individual dots into their 3x3 patterns by using a second custom data structure called a “target”. The target data structure is a linked list and has elements for the number of dots in the pattern, dotData structures for each dot in the pattern, and other data to be generated later such as group position and orientation. To group the dots into targets, the program follows the outlined algorithm.

1.	For each new dot, check each dot inside each existing target.

2.	If there exists a dot in any target such that the new dot is within the maximum spacing between dots, add the new dot to this target.

3.	Else; create a new target and add the new dot to the new target.

We can see that this is not necessary the best method for grouping dots together as it is based on a maximum distance between dots. In fact, this forces the patterns to be a certain distance away from each other to avoid confusion. In concept, the patterns should be at least half the size of the robot to avoid this conflict. The benefits of this classification scheme are its simplicity and speed for computation.

Pattern Identification

Once the contours (dots) have been grouped into the linked list of targets, the targets must be matched to the trained patterns. This data appears extremely robust since the spacing between dots is at such clean and quantized intervals. To match each target to a trained pattern, the algorithm compares all patterns with the same number of dots and searches for the best match. The comparison between patterns with the same number of dots is done with a simple squared differences error calculation. After this process, each region of dots is classified by the global number as trained by the pre-processing algorithm.

Results

To calculate the position and orientation of each target, the camera calibration matrix comes into play. First, the position is calculated by finding the center of mass of each dot in a target in the image frame (pixels). For each dot, the camera calibration matrix is used to transform this data into world coordinates. Finally, the world coordinates of the dots are summed to find the group center of mass. This group center of mass becomes the world coordinates for the target position. To calculate the angle, specific angle information is extracted from the patterns. This angle information is then used in combination with the pre-processed offset angle to generate a group orientation. These two vectors are then sent out to the user-specified serial port.