Difference between revisions of "Mohr's Circle"

Revision as of 15:47, 4 July 2006

Mohr's circle is a tool for analyzing element stress. The drawing below shows mohr's circle and some of the relavent points of interest.

Given a state of stress, $(\sigma _{x},\sigma _{y},\tau _{xy})$ , we can calculate the principle stresses,

$\sigma _{1}={\frac {1}{2}}\left(\sigma _{x}+\sigma _{y}\right)+{\frac {1}{2}}{\sqrt {\left(\sigma _{x}-\sigma _{y}\right)^{2}+4\tau _{xy}^{2}}}$

$\sigma _{2}={\frac {1}{2}}\left(\sigma _{x}+\sigma _{y}\right)-{\frac {1}{2}}{\sqrt {\left(\sigma _{x}-\sigma _{y}\right)^{2}+4\tau _{xy}^{2}}}$

@@ Line 1: / Line 1: @@
 ==Mohr's Circle for 2D==
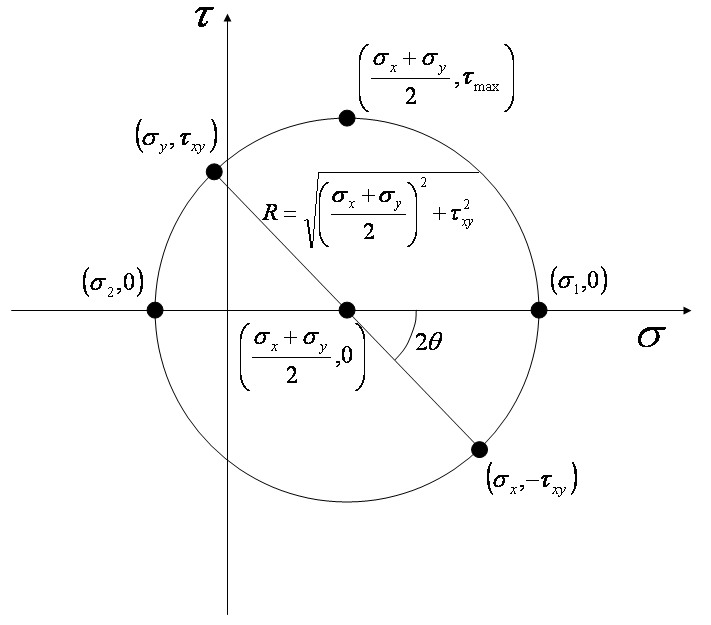
+Mohr's circle is a tool for analyzing element stress.  The drawing below shows mohr's circle and some of the relavent points of interest.
-[[image:mohrs circle.png|center|600px]]
+[[image:mohrs circle.png|center]]
+Given a state of stress, <math>(\sigma_x,\sigma_y,\tau_{xy})</math>, we can calculate the principle stresses,
+<math>\sigma_1=\frac{1}{2}\left(\sigma_x+\sigma_y\right)+\frac{1}{2}\sqrt{\left(\sigma_x-\sigma_y\right)^2+4\tau_{xy}^2}</math>
+<math>\sigma_2=\frac{1}{2}\left(\sigma_x+\sigma_y\right)-\frac{1}{2}\sqrt{\left(\sigma_x-\sigma_y\right)^2+4\tau_{xy}^2}</math>