Difference between revisions of "Passive Filters"
| Line 1: | Line 1: | ||
__TOC__ |
__TOC__ |
||
We can build some very simple filters out of a capacitor and a resistor. A filter |
We can build some very simple filters out of a capacitor and a resistor. A filter blocks some frequencies, while admitting others. |
||
Better filters can be made out of op-amps. |
Better filters can be made out of op-amps. |
||
==Low-Pass Filters (LPF)== |
==Low-Pass Filters (LPF)== |
||
A low |
A low-pass filter admits lower frequencies and blocks out high ones. This can help us smooth out our signals and get rid of high frequency noise. |
||
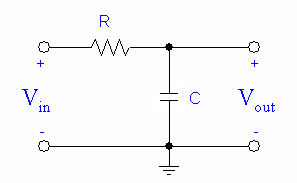
We can make one by hooking up our capacitor and resistor like this: |
We can make one by hooking up our capacitor and resistor like this: |
||
| Line 15: | Line 15: | ||
[[Image:RC_LPF_frequncy_response.gif]] |
[[Image:RC_LPF_frequncy_response.gif]] |
||
As we can see, the filter blocks the higher |
As we can see, the filter blocks the higher frequencies. |
||
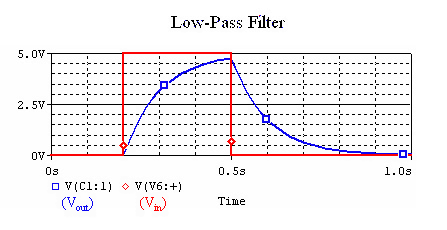
A square wave is made out of a superposition of many sine waves, the low-pass filter blocks out the sine waves with higher frequencies. Our input and output looks like: |
|||
[[Image:RC_LPF_square_wave.gif]](C=200uF, R=500Ω) |
[[Image:RC_LPF_square_wave.gif]](C=200uF, R=500Ω) |
||
==High-Pass Filter (HPF)== |
==High-Pass Filter (HPF)== |
||
A high |
A high-pass filter blocks out lower frequencies while letting high frequencies through. The output signal responds more strongly to changes in the input signal, such as that coming from a motion detector. |
||
We can make a simple high-pass filter by hooking up our capacitor and resistor like this: |
We can make a simple high-pass filter by hooking up our capacitor and resistor like this: |
||
Revision as of 14:21, 6 July 2006
We can build some very simple filters out of a capacitor and a resistor. A filter blocks some frequencies, while admitting others.
Better filters can be made out of op-amps.
Low-Pass Filters (LPF)
A low-pass filter admits lower frequencies and blocks out high ones. This can help us smooth out our signals and get rid of high frequency noise.
We can make one by hooking up our capacitor and resistor like this:
When set R=500Ω and C=2nF, and hook up an AC voltage source, the voltage we see at depends on the frequency of our source. Here is a plot of the frequency response of the filter, on a logarithmic scale from 10Hz to 10MHz:
File:RC LPF frequncy response.gif
As we can see, the filter blocks the higher frequencies.
A square wave is made out of a superposition of many sine waves, the low-pass filter blocks out the sine waves with higher frequencies. Our input and output looks like:
High-Pass Filter (HPF)
A high-pass filter blocks out lower frequencies while letting high frequencies through. The output signal responds more strongly to changes in the input signal, such as that coming from a motion detector.
We can make a simple high-pass filter by hooking up our capacitor and resistor like this:
The frequncy response of a filter with R=500Ω and C=2nF looks like this:
File:RC HPF frequency Response.gif
This time, the filter blocks the lower frequencies.
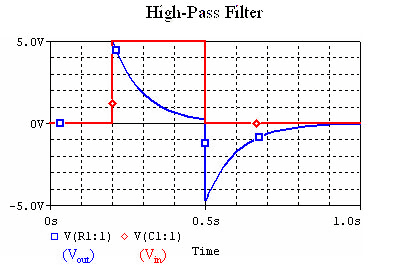
When we put a square wave though the filter, the resulting waveform looks like this:
Notice that when the input voltage drops to zero, the output voltage becomes negative. This is because the capacitor is discharging, and forcing the current backwards.
References
Hayt, William H. Jr., Jack E. Kemmerly, and Steven M. Durbin. Engineering Circuit Analysis. 6th ed. New York:McGraw-Hill, 2002.