Difference between revisions of "Brushed DC Motor Theory"
| Line 23: | Line 23: | ||
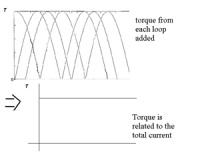
We could also have several commutators and loops. The total torque generated is the sum of all the torques from each of the loops added. |
We could also have several commutators and loops. The total torque generated is the sum of all the torques from each of the loops added. |
||
{| align="center" |
|||
{| |
|||
|- |
|- |
||
| valign="bottom" | [[image:brush.jpg|thumb| |
| valign="bottom" | [[image:brush.jpg|thumb|200px|Motor with several commutators and loops]] |
||
| valign="bottom" | [[image:torque1.jpg|thumb| |
| valign="bottom" | [[image:torque1.jpg|thumb|200px]] |
||
| valign="bottom" | [[image:torque2.jpg|thumb| |
| valign="bottom" | [[image:torque2.jpg|thumb|200px]] |
||
|} |
|} |
||
Revision as of 10:47, 21 June 2006
How A Motor Works
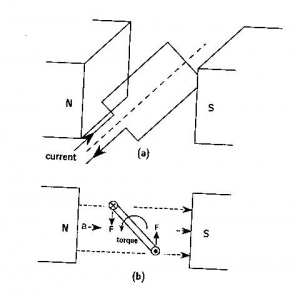
Let's consider a permanent magnet brushed motor. The piece connected to the ground is called the stator and the piece connected to the output shaft is called the rotor. The inputs of the motor are connected to 2 wires and by applying a voltage across them, the motor turns.
The torque of a motor is generated by a current carrying conductor in a magnetic field. The right hand rule states that if you point your right hand fingers along the direction of current, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} , and curl them towards the direction of the magnetic flux, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B} , the direction of force is along the thumb.
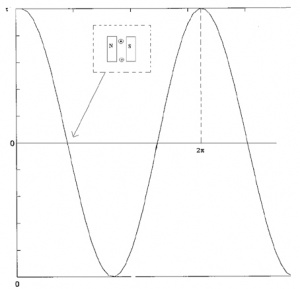
Now, imagine a loop of wire with some resistance is inserted between the two permanent magnets. The following diagrams show how the motor turns:
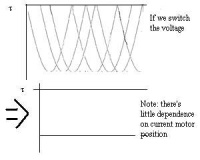
You might be able to notice that the direction of rotation is changing every half cycle. To keep it rotating in the same direction, we have to switch the current direction. The process of switching current is called commutation. To switch the direction of curent, we have to use brushes and commutators. Commutation can also be done electronically (Brushless motors) and a brushless motor usually has a longer life. The following diagram shows how brushes and commutators work.
We could also have several commutators and loops. The total torque generated is the sum of all the torques from each of the loops added.
File:Brush.jpg Motor with several commutators and loops |
Equations
So, the torque is proportional to the current through the windings,
,
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} is the torque, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is the current, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} is a constant. The wire coils have both a resistance, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} , and an inductance, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} . When the motor is turning, the current is switching, causing a voltage,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}V = L \frac{dI}{dt}\end{matrix}}
This voltage is known as the back-emf(electromotive force), Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} . If the angular velocuty of the motor is , then
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}\varepsilon = k\omega\end{matrix}} ,
like a generator. This voltage, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varepsilon} , is working against the voltage we apply across the terminals, and so,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}(V- k\omega) = IR\end{matrix}} ,
where
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}I = \frac{\tau}{R}\end{matrix}}
which implies
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}(V-k\omega) = \frac{\tau}{k}R\end{matrix}} .
The maximum or stall torque is the torque at which Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega = 0} or
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}\tau_{stall} = \frac{kV}{R}\end{matrix}} ,
and the stall or starting current,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}I_{start} = \frac{V}{R}\end{matrix}}
The no load speed,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}\omega_{no-load} = \frac{V}{k}\end{matrix}} ,
is the maximum speed the motor can run. Given a constant voltage, the motor will settle at a constant speed, just like a terminal velocity. If we plot
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{matrix}\omega_{max} = \frac{V}{k} - \frac{\tau}{k^2}R\end{matrix}} ,
we can get the speed-torque curve:
Units
Here are the different units for the torque, current and voltage
| Parameter | Symbol | Common Units |
|---|---|---|
| Torque | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau} | Nm (=kgm/s^2*m), kgfm(=9.8 times Nm), gfcm, mNm, etc |
| Current | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} | Amperes(Amps), mA |
| Voltage | Volts | |
| Mechanical Power | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau\omega} | 1 Nm/sec = 1 watt |
| Electrical Power | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle VI} | 1 volt*amp = 1 watt |