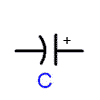Resistors (Ohm's Law), Capacitors, and Inductors

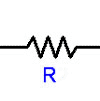
Resistors

The symbol for a resistor:

Real resistors:

Try wikipedia for more on resistors and for the resistor color codes.

The relationship between the current through a conductor with resistance and the voltage across the same conductor is described by Ohm's law:

$V=IR\,$

where V is the voltage across the conductor, I is the current through the conductor, and R is the resistance of the conductor.

The power dissipated by the resistor is equal to the voltage multiplied by the current:

$P=IV\,$

If I is measured in amps and V in volts, then the power P is in watts.

By plugging in different forms of V=IR, we can rewrite P=IV as:

$P=I^{2}R\,$

or

$P={\frac {V^{2}}{R}}.$

Capacitors

The symbol for a capacitor:

or

Real capacitors:

The capacitor on the right is polarized. The potential on the straight side (with the plus sign) should always be higher than the potential on the curved side.

###PUT PICTURE OF CAPACITORS HERE###

A capacitor is a device that stores electric charges. The current through a capacitor can be changed instantly, but it takes time to change the voltage across a capacitor.

The unit of measurement for the capacitance of a capacitor is the farad, which is equal to 1 coulomb per volt.

The charge(q), voltage (v), and capacitance(C) of a capacitor are related as follows:

$q(t)=Cv(t)\,$

where q(t) and v(t) are the values for charge and voltage, expressed as a function of time.

Differentiating both sides with respect to time gives:

$i(t)=C{\frac {dv}{dt}}$

Rearranging and then integrating with respect to time give:

$v(t')={\frac {1}{C}}\int _{t_{0}}^{t'}i(t)dt+v(t_{0})$

If we assume that the charge, voltage, and current of the capacitor are zero at $t_{0}=-\infty$, our equation reduces to:

$v(t')={\frac {1}{C}}\int _{-\infty }^{t'}i(t)dt$

The energy stored in a capacitor (in joules) is given by the equation:

$w_{C}(t)={\frac {1}{2}}Cv^{2}$

Inductors

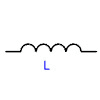
The symbol for an inductor:

An inductor stores energy in the form of a magnetic field, usually by means of a coil of wire. An inductor resists change in the current flowing through it. The voltage across an inductor can be changed instantly, but an inductor will resist a change in current.

Devices with coils of wire, such as motors or transformers, add inductance to a circuit. However, we generally don't purposefully add inductors to circuits.

The relationship between the voltage across the inductor is linearly related by a factor L, the inductance, to the time rate of change of the current through the inductor. The unit for inductance is the henry, and is equal to a volt-second per ampere.

The relationship between the voltage and the current is as follows:

$v(t)=L{\frac {di}{dt}}$

If we multiply both sides by dt, we get:

$di={\frac {1}{L}}vdt$

Integrating both sides from $t_{0}$ to $t'$ gives:

$i(t')-i(t_{0})={\frac {1}{L}}\int _{t_{0}}^{t'}vdt$

which is equal to:

$i(t')={\frac {1}{L}}\int _{t_{0}}^{t'}vdt+i(t_{0})$

assuming that the voltage, current and energy of the inductor are all zero at $t=-\infty$ reduces the equation to

$i(t')={\frac {1}{L}}\int _{-\infty }^{t'}vdt$

The energy stored in the inductor is given by:

$w_{L}(t)={\frac {1}{2}}Li^{2}$

Elements in Series and Parallel

Resistors connected in series and parallel:

Two Elements in Series and Parallel

	Resistor	Capacitor	Inductor
Series	$R_{eq}=R_{1}+R_{2}\,$	$C_{eq}={\frac {C_{1}C_{2}}{C_{1}+C_{2}}}$	$L_{eq}=L_{1}+L_{2}\,$
Parallel	$R_{eq}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}$	$C_{eq}=C_{1}+C_{2}\,$	$L_{eq}={\frac {L_{1}L_{2}}{L_{1}+L_{2}}}$

More than 2 Elements in series or parallel

Here we provide the equations for calculating the equivalant resistance of three or more resistors in parallel; the same form can be applied to the corresponding equations for capacitors and inductors. Of course, you can always just simplify a network of elements by combining two at a time using the equations above.

To find the combined resistance of resistors connected in series, simply add the resistances:

$R_{eq}=R_{1}+R_{2}+\cdot \cdot \cdot +R_{n}$

If the resistors are connected in parallel, the equation is:

${\frac {1}{R_{eq}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdot \cdot \cdot +{\frac {1}{R_{n}}}$

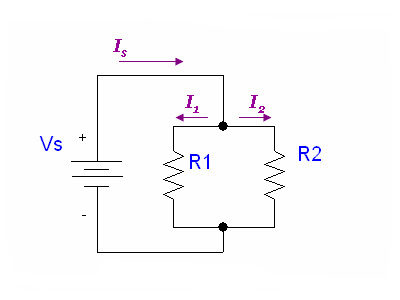
Proof for Resistors in Parallel equation

Here we provide the derivation for the parallel resistors equation. The corresponding equations for capacitors and inductors can be derived with a similar method.

We can prove the equation for parallel resistors by using Kirchhoff's voltage and current laws:

$V_{s}=V_{R1}=V_{R2}\,$   (KVL)

$I_{s}=I_{1}+I_{2}\,$           (KCL)

Plugging in the constitutive law for resistors in the second equation yields:

$I_{s}={\frac {V_{s}}{R_{1}}}+{\frac {V_{s}}{R_{2}}}=V_{s}\left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)=V_{s}\left({\frac {R_{1}+R_{2}}{R_{1}R_{2}}}\right)$

$R_{eq}={\frac {V_{s}}{I_{s}}}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}$

References

Hayt, William H. Jr., Jack E. Kemmerly, and Steven M. Durbin. Engineering Circuit Analysis. 6th ed. New York:McGraw-Hill, 2002.