Difference between revisions of "Brushed DC Motor Theory"
m (→Equations) |
|||
| (127 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Actuators]][[Category:Motors]] |
[[Category:Actuators]][[Category:Motors]] |
||
===How A Motor Works=== |
|||
==Introduction== |
|||
Let's consider a permanent magnet brushed motor. The piece connected to the ground is called the <I>stator</I> and the piece connected to the output shaft is called the <I>rotor</I>. The inputs of the motor are connected to 2 wires and by applying a voltage across them, the motor turns. |
|||
The specific type of motor we are addressing is the permanent magnet brushed DC motor (PMDC). These motors have two terminals. Applying a voltage across the terminals results in a proportional speed of the output shaft in steady state. |
|||
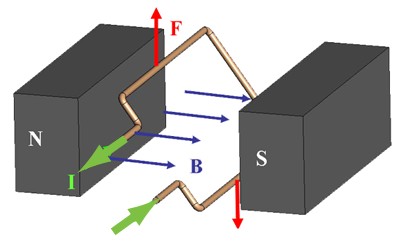
The<I> torque </I>of a motor is generated by a current carrying conductor in a magnetic field. The<I> right hand rule </I>states that if you point your right hand fingers along the direction of current, <math>I</math>, and curl them towards the direction of the magnetic flux, <math>B</math>, the direction of force is along the thumb. |
|||
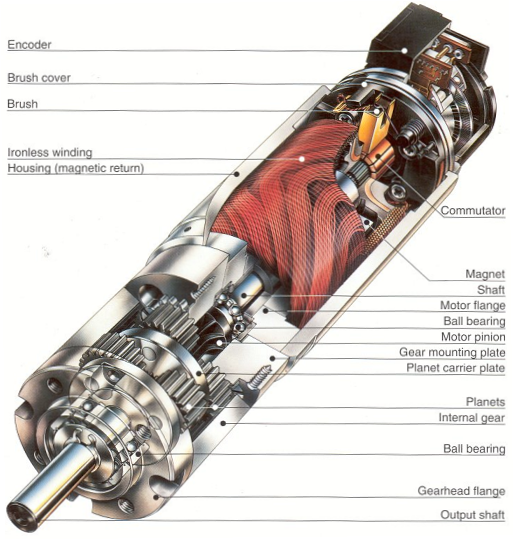
There are two pieces to the motor: 1) ''stator'' and 2) ''rotor''. The ''stator'' includes the housing, permanent magnets, and ''brushes''. The ''rotor'' consists of the output shaft, ''windings'' and ''commutator''. The image below shows a cut-away view of a [http://www.maxonmotor.com Maxon] motor. ''Note this picture has a gearbox and encoder attached to the motor''. |
|||
[[image:Right Hand Rule.jpg|center|400px]] |
|||
[[image:motor cutaway.png|center]] |
|||
Now, imagine a loop of wire with some resistance is inserted between the two permanent magnets. The following diagrams show how |
|||
the motor turns: |
|||
==Motor Physics== |
|||
The forces inside a motor that cause the rotor to rotate are called ''Lorentz Forces''. If an electron is moving through a magnetic field, it experiences a force. If we have a current <math>\vec I</math> passing through a wire in a magnetic field <math>\vec B</math>, the wire experiences a force <math>\vec F</math> proportional to the cross product of the current (expressed as a vector, including the direction of flow) and the magnetic field: |
|||
{| align="center" |
{| align="center" |
||
|<math>\vec F \propto \vec I \times \vec B\,</math> |
|||
|- |
|||
| valign="bottom" | [[image:Motor Operation.jpg|thumb|300px|Diagram showing how the motor works]] |
|||
| valign="bottom" | [[image:sine1.jpg|thumb|300px|Relationship between the Torque and the angle the loop made with the magnet]] |
|||
|} |
|} |
||
You can easily find the direction of this force using the ''Right Hand Rule''. The ''Right Hand Rule'' states that if you point your right hand's index finger along the direction of current, <math>I</math>, and your middle finger in the direction of magnetic flux, <math>B</math>, the direction of force is along the thumb. See the picture below. |
|||
You might be able to notice that the direction of rotation is changing every half cycle. To keep it rotating in the same direction, we have to switch the current direction. The process of switching current is called commutation. To switch the direction of curent, we have to use <I>brushes</I> and <I>commutators</I>. Commutation can also be done electronically (Brushless motors) and a brushless motor usually has a longer life. The following diagram shows how brushes and commutators work. |
|||
[[image:Lorentz Force.png|center]] |
|||
Now, imagine this single wire is replaced with a loop of wire. Between the magnets' poles, this looks like two wires with current flowing in opposite directions. The forces on the wires cause the loop to rotate. |
|||
[[image:Motor_coils_corrected.jpg|center]] |
|||
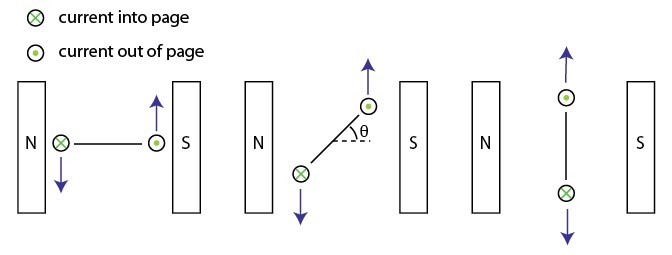
A '''coil''' consists of many such loops, and it is attached to the rotor and rotates. As it does so, the magnitude and direction of the forces on the wires remain approximately constant. However, the resultant torque varies with the angle. Look at the picture below. When the coil starts, there is maximum torque. As the coil moves, the moment arm is reduced and the torque decreases. Finally, when the coil is vertical (in the picture), there is no torque. |
|||
[[image:rotating-coil.jpg|center]] |
|||
<!-- This figure has forces in the wrong direction. |
|||
[[image:rotating coils.png|center]] |
|||
--> |
|||
To keep a nearly constant torque on the rotor, we can do two things. First, we can reverse the current through the coil every half turn. So instead of an alternating torque like the one in the first figure below, the torque is always in the same direction. Also, additional coils can be used. When these coils are offset at different angles around the motor, the resultant torque becomes the sum of the colored torque curves in the figure below. The resultant torque is always greater than zero, but is not constant. This angle-dependent variation is called ''torque ripple''. |
|||
[[image:torque graphs.png|center]] |
|||
The process of switching current direction is called ''commutation''. To switch the direction of curent, brushed DC motors use <I>brushes</I> and <I>commutators</I>. The brushes are attached to the motor's two external wires, and the commutator segments slide over the brushes so that current through the coils switches at appropriate angles. Commutation can also be done electronically (see [[Brushless DC Motors]]). The following diagram shows how brushes and commutators work. A real commutator must have at least three segments. |
|||
[[image:Motor Commutators.jpg|center|400px]] |
[[image:Motor Commutators.jpg|center|400px]] |
||
==Equations== |
|||
We could also have several commutators and loops. The total torque generated is the sum of all the torques from each of the loops added. |
|||
[[image:dc motor power.png|center]] |
|||
{| align="center" |
|||
|- |
|||
| valign="bottom" | [[image:torque1.jpg|300px]] |
|||
| valign="bottom" | [[image:torque2.jpg|300px]] |
|||
|} |
|||
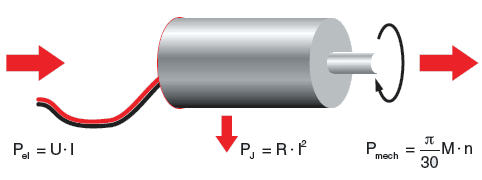
We start by writing the equation for conservation of energy in the motor. The power is input as electrical power, <math>P_{elec}\,</math> and the motor converts that to mechanical power, <math>P_{mech}\,</math>. However, some of the power is lost as heat, <math>P_{heat}\,</math>, due to ohmic heating of the motor coils. |
|||
===Equations=== |
|||
<center><math>P_{elec}=P_{heat}+P_{mech}\,</math></center> |
|||
So, the torque is proportional to the current through the windings, |
|||
<math>\begin{matrix}\tau = k I\end{matrix}</math>, |
|||
We can re-write this in terms of electrical and mechanical quantities as |
|||
where <math>\tau</math> is the torque, <math>I</math> is the current, and <math>k</math> is a constant. The wire coils have both a resistance, <math>R</math>, and an inductance, <math>L</math>. When the motor is turning, the current is switching, causing a |
|||
voltage, |
|||
<math>\begin{matrix}V = L \frac{dI}{dt}\end{matrix}</math> |
|||
<center><math>iv_m=i^2R+\tau\omega\,</math></center> |
|||
This voltage is known as the back-emf(electromotive force), <math>\varepsilon</math>. If the angular velocuty of the motor is <math>\omega</math>, then |
|||
<math>\begin{matrix}\varepsilon = k\omega\end{matrix}</math>, |
|||
where <math>v_m</math> is the voltage across the motor terminals, <math>i</math> is the current through the motor, <math>\tau</math> is the torque produced by the motor, and <math>\omega</math> is its angular velocity. |
|||
The wire coils have both a resistance, <math>R</math>, and an inductance, <math>L</math>. The motor's defining equation is |
|||
<math>\begin{matrix}(V- k\omega) = IR\end{matrix}</math>, |
|||
<center><math>\begin{matrix}v_m = iR + L\frac{di}{dt} + v_{emf} \end{matrix}</math></center> |
|||
where |
|||
where <math>v_{emf}</math> is called the |
|||
<math>\begin{matrix}I = \frac{\tau}{R}\end{matrix}</math> |
|||
''back-emf'' ('''e'''lectro'''m'''otive '''f'''orce). The back-emf is proportional to the speed of the motor, |
|||
<center><math>v_{emf} = \begin{matrix}\frac{n}{k_n}\end{matrix}\,</math></center> |
|||
which implies |
|||
where <math>n</math> is the rotation in '''revolutions-per-minute''' (rpm) (to be consistent with the Maxon datasheet below) and <math>k_n</math> is called the '''speed constant''', the inverse of which is often called the '''electrical constant''' <math>k_e\,</math>, which depends on the motor design. (My preference is to use SI units, using radians-per-second for angular velocity and volt-seconds/radians for the electrical constant and radians/volt-seconds for the speed constant. But speed constants are usually given in different units, and rpms are the most common angular velocity unit in motor data sheets.) The back-emf term indicates that any motor is also a generator: if we spin the motor shaft, we read a voltage at the motor terminals. This is how dams create hydroelectric power. |
|||
<math>\begin{matrix}(V-k\omega) = \frac{\tau}{k}R\end{matrix}</math>. |
|||
The torque generated by the motor is proportional to the current through the windings, where the constant of proportionality is called the '''torque constant''' <math>k_t</math> or '''motor constant''' <math>k_M</math>: |
|||
The maximum or stall torque is the torque at which <math>\omega = 0</math> or |
|||
<math>\ |
<center><math>\tau = k_Mi\,</math></center> |
||
The torque constant has the same numerical value as the inverse of the speed constant when they are expressed in the same SI units (use radians instead of revolutions, seconds instead of minutes, etc.), so there really is just one constant describing how our motor converts current to torque and angular velocity to voltage. To see this, remember the power equality <math>iv_m=i^2R+\tau\omega</math>, divide through by <math>i</math>, and you are left with |
|||
and the stall or starting current, |
|||
<math>v_m = i R + k_M \omega</math>; in other words, <math>k_M \omega</math> has taken the place of <math>v_{emf}=n/k_n</math> in the motor voltage equation (where <math>di/dt=0</math>). |
|||
<!-- This is for non-SI units, as in the Maxon datasheets. |
|||
<math>\begin{matrix}I_{start} = \frac{V}{R}\end{matrix}</math> |
|||
<center><math>k_n \cdot k_M = \begin{matrix} \frac{30,000}{\pi} \end{matrix}\,</math></center> |
|||
--> |
|||
We are often interested in the steady-state operating characteristics of a motor, when the current <math>i</math> is constant. The term <math>L di/dt</math> becomes zero, and we get |
|||
The no load speed, |
|||
<math> |
<center><math>v_m-v_{emf}-iR=0\,</math></center> |
||
which, using the relationships <math>v_{emf} = n/k_n</math> and <math>\tau = k_M i</math>, can be expressed equivalently as |
|||
is the maximum speed the motor can run. Given a constant voltage, the motor will settle at a constant speed, just like a terminal velocity. If we plot |
|||
<math>\begin{matrix |
<center><math>\begin{matrix} n = k_n (v_m - \frac{R}{k_M} \tau)\end{matrix}</math></center> |
||
This equation allows us to plot the '''speed-torque curve''' of a motor. Given a constant <math>v_m</math>, we can plot the speed of the motor as a function of the torque it produces (in steady state). The curve is just a straight line, as illustrated below. This equation allows us to calculate the '''stall''' (or '''starting''') '''torque''', by plugging in <math>n=0</math>. This is the maximum torque the motor can generate. We can also calculate the '''stall current''' by dividing the stall torque by the motor constant (or, equivalently, by dividing <math>v_m</math> by <math>R</math>). This is the maximum current the motor will draw. We can also calculate the '''no-load speed''', the maximum speed the motor will achieve, by assuming it provides zero torque (i.e., there is no friction resisting motion) and plugging in <math>\tau = 0</math>. See the example motor datasheet below. |
|||
<!-- old text |
|||
This back-emf voltage is working against the voltage we apply across the terminals. Using the constants from above, we get this equation, |
|||
<center><math>v=\begin{matrix}\frac{n}{k_n}\end{matrix}+\begin{matrix}\frac{\tau}{k_M}\end{matrix}R\,</math></center> |
|||
The maximum torque, or ''stall torque'', is the torque at which <math>n = 0</math> or |
|||
<center><math>\tau_{stall} = \begin{matrix}\frac{vk_M}{R}\end{matrix}\,</math></center> |
|||
From this we can find the stall current, or ''starting current'', |
|||
<center><math>i_0 = \begin{matrix}\frac{V}{R}\end{matrix}\,</math></center> |
|||
The ''no-load speed'' is the maximum speed the motor can turn. To find its value, we set the torque equal to zero and we get |
|||
<center><math>n_0 = k_nv\,</math></center> |
|||
This relationship means that, given a constant voltage, the motor will settle at a constant speed. This linear relationship produces the ''constant voltage speed-torque line'' |
|||
<center><math>n = n_0 - \begin{matrix}\frac{n_0}{\tau_{stall}}\end{matrix}\tau\,</math></center> |
|||
--> |
|||
==Datasheets and Speed-Torque Curves== |
|||
The datasheet below is for the [[Actuators_Available_in_the_Mechatronics_Lab#6W_Maxon_motor_with_6:1_gearhead_and_100_line_encoder|Maxon motor available in the Mechatronics Lab]]. That motor also has an integrated 6:1 gearhead and a 100 line encoder. The motor is rated at 6 W, which is approximately the input power (voltage times current) when the motor is operated at the nominal voltage (24 V) and maximum continuous torque, where the current is approximately 240 mA. |
|||
[[image:maxon-characteristics-small.jpg|center]] |
|||
'''1.''' Nominal voltage: The recommended maximum voltage across the motor terminals, and the voltage for which the speed-torque curve (below) is plotted. The motor can be powered with less or more voltage, but higher voltage should be used with care, to prevent the motor coils from overheating due to ohmic (resistive) heating. |
|||
'''2.''' No load speed, <math>n_0\,</math>: The speed of the motor powered by the nominal voltage when the motor provides zero torque. |
|||
'''3.''' No load current: The current required to spin the motor at the no load condition (i.e., the current needed to provide the torque necessary to overcome friction). |
|||
'''4.''' Nominal speed: The speed of the motor at the maximum continuous torque. |
|||
'''5.''' Nominal torque (max continuous torque): The maximum torque the motor can provide continuously without overheating. |
|||
'''6.''' Nominal current (max continuous current): The current that yields the maximum continuous torque. This maximum is determined by thermal characteristics of the motor. The power dissipated by the motor as heat is <math>i^2 R</math>. Larger currents are acceptable intermittently, but large continuous currents may cause the motor to overheat. |
|||
'''7.''' Stall torque, <math>\tau_{stall}\,</math>: The maximum torque achievable by the motor at the nominal voltage. This torque is achieved at zero velocity (stall). |
|||
'''8.''' Starting current, <math>i_0\,</math>: The current through the motor at zero velocity, equal to the nominal voltage divided by the terminal resistance. Also called the stall current. |
|||
'''9.''' Max efficiency: The maximum efficiency of the motor in converting electrical power to mechanical power. This maximum efficiency typically occurs at high speed and low torque; the efficiency is zero at zero speed and zero torque, since the mechanical power is <math>\tau \omega</math>. |
|||
'''10.''' Terminal resistance <math>R\,</math>: The resistance of the motor windings. |
|||
'''11.''' Terminal inductance <math>L\,</math>: The inductance of the motor windings. |
|||
'''12.''' Torque (or motor) constant, <math>k_t\,</math> or <math>k_M\,</math>: The constant of proportionality relating current to torque. In SI units (Newton-meters per amp), the torque constant is equivalent to the inverse of the speed constant in SI units (radians per volt-second). |
|||
'''13.''' Speed constant, <math>k_n\,</math> (which is the inverse of the electrical constant <math>k_e\,</math>): The constant of proportionality relating speed to voltage. Equivalent to the inverse of the torque constant when expressed in SI units. |
|||
'''14.''' Speed/torque gradient: A representation of the slope of the speed-torque curve (see graph below), approximately equal to the no load speed divided by the stall torque. |
|||
'''15.''' Mechanical time constant: The time it takes the unloaded motor to reach 63% of its no load speed under a constant voltage, starting from rest. Proportional to the inertia of the rotor and inversely proportional to the square of the the torque constant. |
|||
'''16.''' Rotor inertia: The inertia of the rotating element (the rotor) about the axis of rotation. |
|||
Much of the data sheet can be expressed in the speed-torque curve, plotted for the constant nominal voltage (below). The mechanical power output is the product of the torque and the speed, and is maximized at half the maximum speed and torque. |
|||
[[image:new-speed-torque-small.gif|center]] |
|||
Often you need higher torques but lower speeds in your application. In this case, you can add a gearbox to the motor, as discussed in [[Choosing a Motor and Gearing Combination|Choosing a Motor and Gearing Combination]]. |
|||
<!-- |
|||
The graph below is the dc motor speed-torque graph for a [http://www.maxonusa.com Maxon] brushed DC motor. The dashed line represents the constant voltage speed-torque line. Because of the speed torque relationship, the power is maximum at half stall-torque and half no-load speed. This point is marked on the graph as well. |
|||
we can get the speed-torque curve: |
|||
[[image:dc motor speed torque curve.png|center]] |
[[image:dc motor speed torque curve.png|center]] |
||
Below is part of a datasheet for a series of [http://www.maxonusa.com Maxon] brushed DC motors. In the lab we have several of the 937 model, with an integrated 6:1 gearhead and 100 line encoder. This table gives the the numerical values for the motor properties and constants. |
|||
===Units=== |
|||
[[image:dc motor data.png|center]] |
|||
Here are the different units for the torque, current and voltage |
|||
{| |
|||
! width="100"|Parameter |
|||
{| align="center" style="text-align: center;" |
|||
! width="100"|Symbol |
|||
! width=" |
! width="100" | Line Number |
||
! width="300" | Name |
|||
! width="200" | Symbol |
|||
|- |
|||
| 3 || No-load speed || <math>n_0\,</math> |
|||
|- |
|||
| 4 || Stall torque || <math>\tau_{stall}\,</math> |
|||
|- |
|||
| 5 || Speed/Torque Gradient || <math>\begin{matrix}\frac{n_0}{\tau_{stall}}\end{matrix}\,</math> |
|||
|- |
|||
| 6 || No-load current || |
|||
|- |
|- |
||
| |
| 7 || Starting current || <math>i_0\,</math> |
||
|- |
|- |
||
| |
| 8 || Terminal Resistance || <math>R\,</math> |
||
|- |
|- |
||
| |
| 14 || Torque Constant || <math>k_M\,</math> |
||
|- |
|- |
||
| |
| 15 || Speed Constant || <math>k_n\,</math> |
||
|- |
|- |
||
| |
| 18 || Terminal Inductance || <math>L\,</math> |
||
|} |
|} |
||
--> |
|||
==Other Effects== |
|||
* '''Cogging.''' With no power to the motor, you'll feel the motor shaft bump-bump-bump as you spin it by hand, due to the orientation-dependent attraction of the rotor to the permanent magnets. |
|||
* '''Friction losses.''' |
|||
==References== |
==References== |
||
* Carl R. Nave, "DC Motors," http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/motdc.html |
* Carl R. Nave, "DC Motors," http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/motdc.html |
||
* Maxon Motor Guide ([[media:Maxon Motor Guide.pdf|pdf]]) |
|||
Latest revision as of 19:19, 16 February 2011
Introduction
The specific type of motor we are addressing is the permanent magnet brushed DC motor (PMDC). These motors have two terminals. Applying a voltage across the terminals results in a proportional speed of the output shaft in steady state.
There are two pieces to the motor: 1) stator and 2) rotor. The stator includes the housing, permanent magnets, and brushes. The rotor consists of the output shaft, windings and commutator. The image below shows a cut-away view of a Maxon motor. Note this picture has a gearbox and encoder attached to the motor.
Motor Physics
The forces inside a motor that cause the rotor to rotate are called Lorentz Forces. If an electron is moving through a magnetic field, it experiences a force. If we have a current passing through a wire in a magnetic field , the wire experiences a force proportional to the cross product of the current (expressed as a vector, including the direction of flow) and the magnetic field:
You can easily find the direction of this force using the Right Hand Rule. The Right Hand Rule states that if you point your right hand's index finger along the direction of current, , and your middle finger in the direction of magnetic flux, , the direction of force is along the thumb. See the picture below.
Now, imagine this single wire is replaced with a loop of wire. Between the magnets' poles, this looks like two wires with current flowing in opposite directions. The forces on the wires cause the loop to rotate.
A coil consists of many such loops, and it is attached to the rotor and rotates. As it does so, the magnitude and direction of the forces on the wires remain approximately constant. However, the resultant torque varies with the angle. Look at the picture below. When the coil starts, there is maximum torque. As the coil moves, the moment arm is reduced and the torque decreases. Finally, when the coil is vertical (in the picture), there is no torque.
To keep a nearly constant torque on the rotor, we can do two things. First, we can reverse the current through the coil every half turn. So instead of an alternating torque like the one in the first figure below, the torque is always in the same direction. Also, additional coils can be used. When these coils are offset at different angles around the motor, the resultant torque becomes the sum of the colored torque curves in the figure below. The resultant torque is always greater than zero, but is not constant. This angle-dependent variation is called torque ripple.
The process of switching current direction is called commutation. To switch the direction of curent, brushed DC motors use brushes and commutators. The brushes are attached to the motor's two external wires, and the commutator segments slide over the brushes so that current through the coils switches at appropriate angles. Commutation can also be done electronically (see Brushless DC Motors). The following diagram shows how brushes and commutators work. A real commutator must have at least three segments.
Equations
We start by writing the equation for conservation of energy in the motor. The power is input as electrical power, and the motor converts that to mechanical power, . However, some of the power is lost as heat, , due to ohmic heating of the motor coils.
We can re-write this in terms of electrical and mechanical quantities as
where is the voltage across the motor terminals, is the current through the motor, is the torque produced by the motor, and is its angular velocity.
The wire coils have both a resistance, , and an inductance, . The motor's defining equation is
where is called the back-emf (electromotive force). The back-emf is proportional to the speed of the motor,
where is the rotation in revolutions-per-minute (rpm) (to be consistent with the Maxon datasheet below) and is called the speed constant, the inverse of which is often called the electrical constant , which depends on the motor design. (My preference is to use SI units, using radians-per-second for angular velocity and volt-seconds/radians for the electrical constant and radians/volt-seconds for the speed constant. But speed constants are usually given in different units, and rpms are the most common angular velocity unit in motor data sheets.) The back-emf term indicates that any motor is also a generator: if we spin the motor shaft, we read a voltage at the motor terminals. This is how dams create hydroelectric power.
The torque generated by the motor is proportional to the current through the windings, where the constant of proportionality is called the torque constant or motor constant :
The torque constant has the same numerical value as the inverse of the speed constant when they are expressed in the same SI units (use radians instead of revolutions, seconds instead of minutes, etc.), so there really is just one constant describing how our motor converts current to torque and angular velocity to voltage. To see this, remember the power equality , divide through by , and you are left with ; in other words, has taken the place of in the motor voltage equation (where ).
We are often interested in the steady-state operating characteristics of a motor, when the current is constant. The term becomes zero, and we get
which, using the relationships and , can be expressed equivalently as
This equation allows us to plot the speed-torque curve of a motor. Given a constant , we can plot the speed of the motor as a function of the torque it produces (in steady state). The curve is just a straight line, as illustrated below. This equation allows us to calculate the stall (or starting) torque, by plugging in . This is the maximum torque the motor can generate. We can also calculate the stall current by dividing the stall torque by the motor constant (or, equivalently, by dividing by ). This is the maximum current the motor will draw. We can also calculate the no-load speed, the maximum speed the motor will achieve, by assuming it provides zero torque (i.e., there is no friction resisting motion) and plugging in . See the example motor datasheet below.
Datasheets and Speed-Torque Curves
The datasheet below is for the Maxon motor available in the Mechatronics Lab. That motor also has an integrated 6:1 gearhead and a 100 line encoder. The motor is rated at 6 W, which is approximately the input power (voltage times current) when the motor is operated at the nominal voltage (24 V) and maximum continuous torque, where the current is approximately 240 mA.
1. Nominal voltage: The recommended maximum voltage across the motor terminals, and the voltage for which the speed-torque curve (below) is plotted. The motor can be powered with less or more voltage, but higher voltage should be used with care, to prevent the motor coils from overheating due to ohmic (resistive) heating.
2. No load speed, : The speed of the motor powered by the nominal voltage when the motor provides zero torque.
3. No load current: The current required to spin the motor at the no load condition (i.e., the current needed to provide the torque necessary to overcome friction).
4. Nominal speed: The speed of the motor at the maximum continuous torque.
5. Nominal torque (max continuous torque): The maximum torque the motor can provide continuously without overheating.
6. Nominal current (max continuous current): The current that yields the maximum continuous torque. This maximum is determined by thermal characteristics of the motor. The power dissipated by the motor as heat is . Larger currents are acceptable intermittently, but large continuous currents may cause the motor to overheat.
7. Stall torque, : The maximum torque achievable by the motor at the nominal voltage. This torque is achieved at zero velocity (stall).
8. Starting current, : The current through the motor at zero velocity, equal to the nominal voltage divided by the terminal resistance. Also called the stall current.
9. Max efficiency: The maximum efficiency of the motor in converting electrical power to mechanical power. This maximum efficiency typically occurs at high speed and low torque; the efficiency is zero at zero speed and zero torque, since the mechanical power is .
10. Terminal resistance : The resistance of the motor windings.
11. Terminal inductance : The inductance of the motor windings.
12. Torque (or motor) constant, or : The constant of proportionality relating current to torque. In SI units (Newton-meters per amp), the torque constant is equivalent to the inverse of the speed constant in SI units (radians per volt-second).
13. Speed constant, (which is the inverse of the electrical constant ): The constant of proportionality relating speed to voltage. Equivalent to the inverse of the torque constant when expressed in SI units.
14. Speed/torque gradient: A representation of the slope of the speed-torque curve (see graph below), approximately equal to the no load speed divided by the stall torque.
15. Mechanical time constant: The time it takes the unloaded motor to reach 63% of its no load speed under a constant voltage, starting from rest. Proportional to the inertia of the rotor and inversely proportional to the square of the the torque constant.
16. Rotor inertia: The inertia of the rotating element (the rotor) about the axis of rotation.
Much of the data sheet can be expressed in the speed-torque curve, plotted for the constant nominal voltage (below). The mechanical power output is the product of the torque and the speed, and is maximized at half the maximum speed and torque.
Often you need higher torques but lower speeds in your application. In this case, you can add a gearbox to the motor, as discussed in Choosing a Motor and Gearing Combination.
Other Effects
- Cogging. With no power to the motor, you'll feel the motor shaft bump-bump-bump as you spin it by hand, due to the orientation-dependent attraction of the rotor to the permanent magnets.
- Friction losses.
References
- Carl R. Nave, "DC Motors," http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/motdc.html
- Maxon Motor Guide (pdf)