Difference between revisions of "Basic Linear Circuits Review"
m |
|||
| (35 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ |
|||
==Common Measurements and Units== |
|||
In the representations of measurements such as charge, voltage, current, and power, an uppercase letter (C, V, I, P) implies that it is constant, and a lowercase letter (c,v,i,p) implies that it is time-variant. |
|||
===Charge (Coulomb)=== |
|||
Protons are positive charges, and electrons are negative charges. Charges in motion is a current. The SI unit for charge is the ''coulomb'', which is equivalent to the amount of charge the current (in amperes) delivers in an amount of time (in seconds). 1 coulomb is equal to 1 ampere multiplied by 1 second. |
|||
<math>1C=(1A)\cdot(1s)</math> |
|||
===Electric Potential (Volt)=== |
|||
The ''volt'' is a unit for the relative potential energy between two points or two electrodes. The ground is usually assigned a voltage of 0, and used as a reference. Current tends to flow from high voltage to low voltage. Voltage is also known as "electro-motive force," or EMF. |
|||
1 volt is equal to 1 joule per coulomb. |
|||
<math>1V=\frac{1J}{1C}</math> |
|||
===Current (Ampere)=== |
|||
An electric current represents electric charges flowing through a conductor. The ''ampere'', or ''amp'', is the unit for the current, and is determined by the rate of flow of the charges. 1 amp is equal to 1 coulomb per second. |
|||
<math>1A=\frac{1C}{1s}</math> |
|||
or |
|||
<math>i(t)=\frac{dq}{dt}</math> |
|||
Since current is the rate of charge flowing through a certain cross section of conductor, we can get the total charge that has flowed through the same cross section over a period of time by integrating the current over time. |
|||
<math>q(t)=\int_{t_0}^{t} i(t) dt</math> |
|||
===Power (Watt)=== |
|||
The power absorbed or produced by a component is the rate at which it expends or generates energy. The SI unit for power is the ''watt'', and 1 watt is equal to 1 joule per second. Written in terms of voltage and current, the power is equal to the voltage across the component multiplied by the current through the component. Thus, we get: |
|||
<math>P=IV\,</math> |
|||
If we check the units for the equation above, we get: |
|||
<math>W=\frac{C}{s} \cdot \frac{J}{C}=\frac{J}{s}</math> |
|||
===Resistance (Ohm)=== |
|||
The unit of measurement for the resistance of a resistor is the ''ohm'', which is equal to 1 volt per amp. |
|||
<math>1\Omega = \frac{1V}{1A}</math> |
|||
===Capacitance (Farad)=== |
|||
The unit of measurement for the capacitance of a capacitor is the ''farad'', which is equal to 1 coulomb per volt. The voltage across a capacitor is proportional to the amount of charge stored (i.e., the time-integral of current). Most capacitors have capacitances much less than a farad, often measured in picofarads or microfarads. A capacitor with a large capacitance stores a lot of electric charge without much voltage across it. |
|||
<math>1F=\frac{1C}{1V}</math> |
|||
===Inductance (Henry)=== |
|||
The unit of measurement for the inductance of an inductor is the ''henry'', which is equal to 1 volt-second per ampere. The voltage across an inductor is proportional to the rate of change of current (measured in amps/second) through it. The larger the inductance, the larger the voltage across the inductor for the same rate of change of current. If current is flowing left to right through an inductor and increasing (respectively decreasing) with time, then the potential on the left side of the inductor is higher (respectively lower) than the potential on the right side. |
|||
<math>1H=\frac{1V\cdot 1s}{1A}</math> |
|||
==Common Electrical Components== |
|||
{| border="1" cellspacing="0" cellpadding="5" align="center" |
{| border="1" cellspacing="0" cellpadding="5" align="center" |
||
|+ Symbols, Variables, and Units |
|+ Symbols, Variables, and Units |
||
|- |
|- |
||
! |
! !! symbol !! variable !! units |
||
|- |
|- |
||
| |
| current source || [[Image:current_source_symbol.gif]] || I || Ampere (A) |
||
|- |
|- |
||
| |
| voltage source || [[Image:voltage_source_round_symbol.gif]] or [[Image:voltage_source_batt_symbol.gif]] || V || Volt (V) |
||
|- |
|- |
||
| resistor || [[Image:resistor_symbol.gif]] || R || Ohm (<math>\Omega</math>) |
|||
| voltage || [[Image:voltage_source_round_symbol.jpg]] or [[Image:voltage_source_batt_symbol.jpg]] <br> (voltage source) || V || Volt (V) |
|||
|- |
|||
| capacitor || [[Image:capacitor_symbol.gif]] or [[Image:capacitor_polarized_symbol.gif]] (polarized)|| C || Farad (F) |
|||
|- |
|- |
||
| |
| Inductor || [[Image:inductor_symbol.gif]] || L || Henry (H) |
||
|- |
|- |
||
| |
| Ground || [[Image:ground_symbol.gif]] || GND || |
||
|- |
|||
|} |
|||
==Mechanical Analogs for Resistors, Capacitors, and Inductors== |
|||
{| border="1" cellspacing="0" cellpadding="5" align="center" |
|||
|- |
|- |
||
!mechanical !! constitutive equation !! electrical !! constitutive equation |
|||
| Inductor || [[Image:inductor_symbol.jpg]] || L || Henry (H) |
|||
|- |
|- |
||
|damper || <math>f=bv\,</math> || resistor || <math>v=Ri\,</math> |
|||
|- |
|||
|spring || <math>f=k\int vdt </math> || capacitor || <math>v=\frac{1}{C}\int idt</math> |
|||
|- |
|||
|mass || <math>f=m\frac{dv}{dt}</math> || inductor || <math>v=L\frac{di}{dt} </math> |
|||
|} |
|||
In the table above, <math>v</math> is velocity for mechanical systems and voltage for electrical systems. Force and voltage are ''effort'' variables. |
|||
Velocity and current are ''flow'' variables. |
|||
==References== |
|||
Hayt, William H. Jr., Jack E. Kemmerly, and Steven M. Durbin. <u>Engineering Circuit Analysis</u>. 6th ed. New York:McGraw-Hill, 2002. |
|||
Latest revision as of 12:53, 19 December 2009
Common Measurements and Units
In the representations of measurements such as charge, voltage, current, and power, an uppercase letter (C, V, I, P) implies that it is constant, and a lowercase letter (c,v,i,p) implies that it is time-variant.
Charge (Coulomb)
Protons are positive charges, and electrons are negative charges. Charges in motion is a current. The SI unit for charge is the coulomb, which is equivalent to the amount of charge the current (in amperes) delivers in an amount of time (in seconds). 1 coulomb is equal to 1 ampere multiplied by 1 second.
Electric Potential (Volt)
The volt is a unit for the relative potential energy between two points or two electrodes. The ground is usually assigned a voltage of 0, and used as a reference. Current tends to flow from high voltage to low voltage. Voltage is also known as "electro-motive force," or EMF. 1 volt is equal to 1 joule per coulomb.
Current (Ampere)
An electric current represents electric charges flowing through a conductor. The ampere, or amp, is the unit for the current, and is determined by the rate of flow of the charges. 1 amp is equal to 1 coulomb per second.
or
Since current is the rate of charge flowing through a certain cross section of conductor, we can get the total charge that has flowed through the same cross section over a period of time by integrating the current over time.
Power (Watt)
The power absorbed or produced by a component is the rate at which it expends or generates energy. The SI unit for power is the watt, and 1 watt is equal to 1 joule per second. Written in terms of voltage and current, the power is equal to the voltage across the component multiplied by the current through the component. Thus, we get:
If we check the units for the equation above, we get:
Resistance (Ohm)
The unit of measurement for the resistance of a resistor is the ohm, which is equal to 1 volt per amp.
Capacitance (Farad)
The unit of measurement for the capacitance of a capacitor is the farad, which is equal to 1 coulomb per volt. The voltage across a capacitor is proportional to the amount of charge stored (i.e., the time-integral of current). Most capacitors have capacitances much less than a farad, often measured in picofarads or microfarads. A capacitor with a large capacitance stores a lot of electric charge without much voltage across it.
Inductance (Henry)
The unit of measurement for the inductance of an inductor is the henry, which is equal to 1 volt-second per ampere. The voltage across an inductor is proportional to the rate of change of current (measured in amps/second) through it. The larger the inductance, the larger the voltage across the inductor for the same rate of change of current. If current is flowing left to right through an inductor and increasing (respectively decreasing) with time, then the potential on the left side of the inductor is higher (respectively lower) than the potential on the right side.
Common Electrical Components
| symbol | variable | units | |
|---|---|---|---|
| current source | 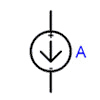 |
I | Ampere (A) |
| voltage source | 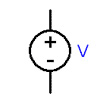 or or  |
V | Volt (V) |
| resistor | 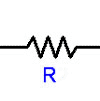 |
R | Ohm () |
| capacitor |  or or 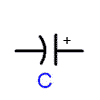 (polarized) (polarized) |
C | Farad (F) |
| Inductor | 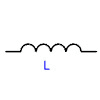 |
L | Henry (H) |
| Ground | 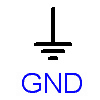 |
GND |
Mechanical Analogs for Resistors, Capacitors, and Inductors
| mechanical | constitutive equation | electrical | constitutive equation |
|---|---|---|---|
| damper | resistor | ||
| spring | capacitor | ||
| mass | inductor |
In the table above, is velocity for mechanical systems and voltage for electrical systems. Force and voltage are effort variables. Velocity and current are flow variables.
References
Hayt, William H. Jr., Jack E. Kemmerly, and Steven M. Durbin. Engineering Circuit Analysis. 6th ed. New York:McGraw-Hill, 2002.

















