VPOD 3DOF Vibratory Device
Nondimensional 3DOF Bouncing Ball Simulator
Introduction
The Nondimensional 3DOF Bouncing Ball Simulator is a simple Matlab program meant to mimic the behavior of a bouncing ball on a vibratory device capable of sinusoidal motion in three degrees, such as the VPOD. The simulator uses a numerical method in which the equations of motion describing the ball's flight are determined from the state variables of the previous impact. The program uses a binary search to locate the time at which the ball's position in the x,z plane is equal to that of the oscillating bar. In short, it calculates the intersection of a parabola with a sinusoid, uses a simple impact model to compute the new state variables, and repeats this computation as many times as desired. The equations of motion for the oscillating bar are as follows:
where A_x, A_z, A_theta represent the maximum x, z, and angular displacements of the bar's motion. The key input variables are the three position amplitudes, three frequencies, and three phase angles, as well as coefficients of restitution in the normal and tangential directions.
Quick Start
In order to run the simulator, first download the Matlab files by clicking on the link below:
Description of Functions
The zipped folder contains 6 m-files:
- bBallSim - This is the main m-file and likely the only one you will have to worry about. It contains a big for loop which takes the initial conditions for the ball's flight and calculates one bar impact, storing the data in the matrix 'P'. The post-impact conditions then become the new initial conditions. It loops as many times as indicated.
- binSrch - Uses a binary search method to locate the time where in ball intersects the bar, based off of the initial flight conditions and parameters. It returns the time of intersection (denoted 't2').
- checkLocking - Determines whether or not the ball is locking. Locking is a phenomenon in which the ball's velocity decays to zero, undergoing an infinite number of bounces in the absorbing region of the bar's motion. If the flight time is less than an arbitrarily small value, the ball is determined to be locking, and a value of 1 is returned.
- impact - This function takes the initial conditions and time of impact as inputs. It uses a simple impact model to calculate the post-impact positions and velocities of the ball.
- calculateLaunch - Determines whether or not the ball will be relaunched after locking. If the motion of the bar, and the position of the ball are such that the vertical acceleration of the bar will exceed gravity at some point during its periodic motion, then the ball will be relaunched. Otherwise, the ball will never be relaunched, and the simulation will terminate.
- plotTraj - This function is used only to plot the trajectories of the ball and the bar. This is only used as a visual aid and is helpful for debugging. It can easily be turned off to speed up the simulation.
Explanation of Important Inputs & Parameters
First, open the bBallSim m-file. The first few lines will look like this:
function [P, N] = bBallSim(A_x, A_z, A_th, p) % SYSTEM PARAMETERS num_impacts = 500; % Number of impacts simulator will calculate before terminating A = [A_x; A_z; A_th]; % Position amplitude of bar, nondimensional [A_x, A_z, A_th] phi = [pi/2; pi/2; p]; % Phase angle of bar [phi_x, phi_z, phi_th] f = [1; 2; 1]; % Frequencies of bar motions [f_x, f_z, f_th] w = 2*pi.*f; % [w_x, w_z, w_th]
There are four important inputs for this version of the program.
- A_x is the nondimensionalized position amplitude of the bar in the x (horizontal) direction.
- A_z is the nondimensionalized position amplitude of the bar in the z (vertical) direction.
- A_th is the amplitude in the theta direction (angular about the y). It is already dimensionless.
- p is the relative phase between the theta motion and the other motions.
Nondimensionalizations are as follows:
Position: where f(1) is equal to the first frequency in the vector f (or the horizontal frequency) and g is equal to the acceleration due to gravity
Velocity:
Acceleration:
Simple Test
For example, if one were to input the following:
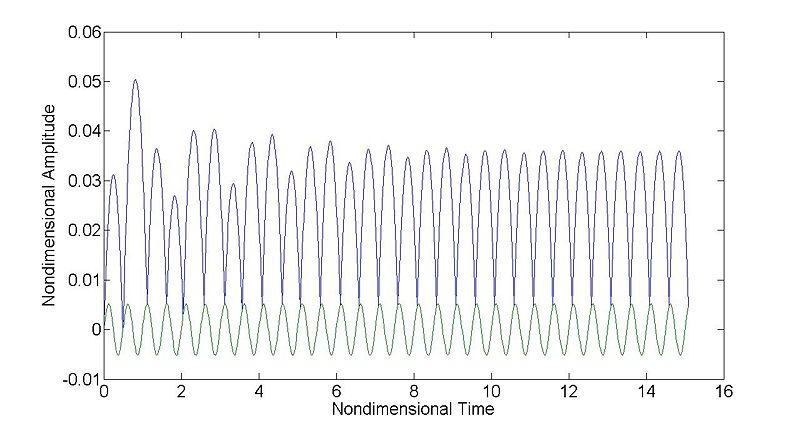
[P, N] = bBallSim(0, 0.0052, 0, 0);
This is setting a motion with zero amplitude in the x and theta directions. 0.0052 is the nondimensional equivalent of 8m/s^2 in the z direction. If this simulation is run for 100 impacts with e = [0.8 0.8], the following plot will be created:
399 Write-up and Raw Data
The following is a 399 Write-up from a 2009-2010 independent study conducted by Undergraduate Eric Bell. The paper uses data from both physical experimentation as well as the simulator described above. EBell-399FinalWriteup
The write-up is also available as a word document EBell-399FinalWriteup Microsoft Word version
Some of the data used in the write-up are included below:
The following contains both the raw data from the real and virtual cameras as well as the calculated a workspace containing the calculated 3D coordinates. This data was used to create Figures 2.3 through 2.5: Figure2.3-2.5 Data The zipped folder also contains the Matlab Figure files corresponding to the plots used in the paper.
The following contains the Matlab workspaces used to create Figures 3.1-3.5. The period 1 and period 2 examples were captured using 2D imaging, whereas the period 3 example uses 3D. Figure files are also included. Figures3.1-3.5 Data
The following is experimental data used to create the bifurcation diagrams shown in Figure 3.8 and 3.10. This data was also used for the examples of period 1 and period 2 m=2 behavior corresponding to Figures 3.6 and 3.7 in the write-up: Data for Bifurcation Diagrams This data was collected using 3 regions of interest (XZ- raw data from real camera, YZ- raw data from "virtual" camera, bar_tracking- raw data for bar's motion using real camera). This workspace also contains the calculated 3D coordinates of the ball (XYZ_BALL) as well as the adjusted coordinates of the bar (XZ_BAR). The Matlab function used to calculate these coordinates is pasted below.
The data for the experiment shown in Figure 3.12 can be downloaded here along with the plot. Data for Figure 3.12 In the workspace, the variable referred to as tau in the plot is saved as "ndPhase."
Other figures included in the paper: Miscellaneous Figures
% The function "calc_coords" takes as inputs, the raw data for vision in
% the XZ and XY planes.
% CC_xz and CC_yz are vectors of size [2x1] containing the principal points
% for each vision plane. Coordinates for principal point should be computed beforehand and reported in
% metric.
% FC_xz and FC_yz are vectors of size [2x1] containing the two focal
% lengths of the lens for each vision plane. These are obtained from the
% Calibration Toolbox and should be left in pixels.
% The function returns a matrix of size [nx5] containing the least squares
% approximation of the (x,y,z) coordinates based off of the vectors from
% the two cameras, as well as the index and time at which these coordinates
% occur.
% NOTES:
% - All computations are done in metric. (Based off of calibration grid)
% - The XZ vision plane = "Real Camera"
% - The YZ vision plane = "Virtual Camera"
function [XYZ_BALL, XZ_BAR] = calc_coords3ROI(XZ, YZ, bar_tracking);
% Should be most recent calibration
w = cd;
calib = '8-17-09 Calibration Constants';
cd('C:\Documents and Settings\John Shih\Desktop\VPOD- EBell\Calibration Constants\');
load(calib);
% Change directory to regular working directory
cd(w);
matSize_xz = size(XZ);
num_datapoints_xz = matSize_xz(1,1);
matSize_yz = size(YZ);
num_datapoints_yz = matSize_yz(1,1);
num_datapoints = min(num_datapoints_xz, num_datapoints_yz);
XYZ_BALL = zeros(num_datapoints-1, 5); % Initialize destination matrix
conv_xz = [FC_xz(1,1) + FC_xz(2,1)] / [CONSTANTS_xz(1,1) + CONSTANTS_xz(3,1)]; % Conversion factor (number of pixels / mm) for vision in XZ
conv_yz = [FC_yz(1,1) + FC_yz(2,1)] / [CONSTANTS_yz(1,1) + CONSTANTS_yz(3,1)];; % Conversion factor (number of pixels / mm) for vision in YZ
dist_origin_xz = [(FC_xz(1,1) + FC_xz(2,1)) / 2] / [conv_xz]; % Taking an average of the two focal lengths,
dist_origin_yz = [(FC_yz(1,1) + FC_yz(2,1)) / 2] / [conv_yz]; % Multiplying by conversion factor to get
% the distance to the calibration grid in metric.
prinP_xz = [CC_xz(1,1); -dist_origin_xz; CC_xz(2,1)]; % [3X1] vector containing the coordinates of the principal points
prinP_yz = [dist_origin_yz; -CC_yz(1,1); CC_yz(2,1)]; % for the "Real" and "Virtual" Cameras.
for i = [1 : 1 : num_datapoints - 1]
planeP_xz = [XZ(i,3); 0; XZ(i,4)]; % [3x1] vector containing the points in the plane of the calibration grid
planeP_yz = [0; -(YZ(i,3)+(2/3)*[YZ(i+1,3) - YZ(i,3)]); (YZ(i,4)+(2/3)*[YZ(i+1,4) - YZ(i,4)])];
x1_xz = prinP_xz(1,1);
y1_xz = prinP_xz(2,1);
z1_xz = prinP_xz(3,1);
x1_yz = prinP_yz(1,1);
y1_yz = prinP_yz(2,1);
z1_yz = prinP_yz(3,1);
x2_xz = planeP_xz(1,1);
y2_xz = planeP_xz(2,1);
z2_xz = planeP_xz(3,1);
x2_yz = planeP_yz(1,1);
y2_yz = planeP_yz(2,1);
z2_yz = planeP_yz(3,1);
% Set up matrices to solve matrix equation Ac = b, where c = [x, y, z]
A_xz = [ (y2_xz - y1_xz), (x1_xz - x2_xz), 0;
(z2_xz - z1_xz), 0, (x1_xz - x2_xz);
0, (z2_xz - z1_xz), (y1_xz-y2_xz) ];
b_xz = [ x1_xz*(y2_xz - y1_xz) + y1_xz*(x1_xz - x2_xz);
x1_xz*(z2_xz - z1_xz) + z1_xz*(x1_xz - x2_xz);
y1_xz*(z2_xz - z1_xz) + z1_xz*(y1_xz - y2_xz) ];
A_yz = [ (y2_yz - y1_yz), (x1_yz - x2_yz), 0;
(z2_yz - z1_yz), 0, (x1_yz - x2_yz);
0, (z2_yz - z1_yz), (y1_yz-y2_yz) ];
b_yz = [ x1_yz*(y2_yz - y1_yz) + y1_yz*(x1_yz - x2_yz);
x1_yz*(z2_yz - z1_yz) + z1_yz*(x1_yz - x2_yz);
y1_yz*(z2_yz - z1_yz) + z1_yz*(y1_yz - y2_yz) ];
A = [A_xz; A_yz];
b = [b_xz; b_yz];
c = A\b; % Solve for 3D coordinates
XYZ_BALL(i, 1) = i;
XYZ_BALL(i, 2) = XZ(i,2);
XYZ_BALL(i, 3) = c(1,1);
XYZ_BALL(i, 4) = c(2,1);
XYZ_BALL(i, 5) = c(3,1);
end
num_datapoints_bar = size(bar_tracking, 1);
offset = 38.5; % Distance from the calibration plane to the plane, coinciding with the front face of the bar (in mm)% the distance to the calibration grid in metric.
XZ_BAR = zeros(num_datapoints_bar, 4);
for i = [1 : 1 : num_datapoints_bar]
XZ_BAR(i,1) = bar_tracking(i,1);
XZ_BAR(i,2) = bar_tracking(i,2);
XZ_BAR(i,3) = bar_tracking(i,3)*(dist_origin_xz - offset) / dist_origin_xz;
XZ_BAR(i,4) = bar_tracking(i,4)*(dist_origin_xz - offset) / dist_origin_xz;
end
%plot(XYZ_BALL(:,2)/(10^6), XYZ_BALL(:,5)-BALL0, XZ_BAR(:,2)/(10^6), XZ_BAR(:,4)-BAR0)