Stability of an Assembly Project
This page describes the "Stability of an Assembly" Project from the Coursera course "Modern Robotics, Course 5: Robot Manipulation and Wheeled Mobile Robots."
Introduction
Your assignment will be graded on:
- An evaluation of your source code, including its clarity for the reader.
- The correctness of your code's output on example assemblies, as well as your physical explanation for the results.
Program Specification
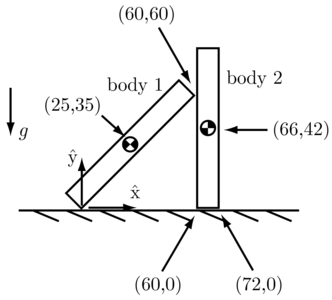
You will write a program to determine if an assembly of planar rigid bodies, in frictional contact with each other, can remain standing in gravity (where gravity acts in the direction), or if the assembly must collapse. (See Example 12.11 and Figure 12.27 in Chapter 12.3 of the book.) An example assembly is shown in the image at right.
Your program will take as input:
- a description of the static mass properties of each of the bodies: the location of the center of mass and the total mass (e.g., in kg); and
- a description of the contacts. Each contact consists of a list of the two bodies involved in the contact (0 means stationary ground, 1 means body 1, 2 means body 2, etc.); the (x,y) location of the contact; the contact normal direction into the first body involved in the contact (this direction could be specified in degrees or radians, for example); and the friction coefficient at the contact. For example, in the image shown, the single contact between body 1 and body 2 could be specified as (1, 2, 60, 60, 3.1416, 0.5). This means the contact is between body 1 and 2, the contact location is at (60,60), the angle of the contact normal pointing into the first body in the list (body 1) is at pi radians, and the friction coefficient is 0.5. One of the contacts between body 0 (ground) and body 2 could be specified as (2, 0, 72, 0, 1.5708, 0.25), indicating that the contact normal into body 2 is at pi/2 radians and the friction coefficient is 0.25.
Ideally your input would be in an argument to the program function call, or in an easily edited external file that can be read by the program.
The output of your program will be binary: it is either possible or impossible for the assembly to remain standing. Your solution method is likely to use linear programming (linprog in MATLAB, LinearProgramming in Mathematica, or scipy.optimize.linprog in Python). If you find a solution to the contact vector (see Example 12.11) and standing is possible, then it is recommended that you also output . This represents one set of contact forces that would keep the assembly standing.
- Important note for Python users: A Coursera student mentioned a bug in an earlier version of linprog, apparently occurring when using the 'simplex' method for solving linear programs where the equality constraints are specified by a matrix that is not full rank. One solution is to use the interior point method by adding the option "method='interior-point'". See the discussion at https://github.com/scipy/scipy/issues/6690.
Unlike the form and force closure linear programming tests, where the elements of your contact vector had to be greater than or equal to a positive value, in this problem the elements of your contact vector only need to be nonnegative. (You are only trying to find one solution to the assembly equilibrium equations; in the form and force closure tests, you needed to show that the contacts could create arbitrary wrenches.)
Your biggest job in this programming assignment is taking the specifications of the bodies' mass properties and the contacts and turning them into static equilibrium equations of the form , similar to Example 12.11 in the book. These equations are solved by linear programming with the constraint that the elements of the contact vector must all be nonnegative. If you have bodies in the assembly, you will have wrench balance equations, and if you have contacts, you will have friction cone edges and therefore elements in your contact vector .
Testing Your Program
First test your program using the assembly shown in the image at the top of the page. Your only freedoms in specifying the assembly are the masses of the bodies and the friction coefficients at the contacts.
- Collapsing assembly. First choose the mass of body 1 to be 2, the mass of body 2 to be 5, the friction coefficients involving body 2 to be 0.5, and the friction coefficient between body 1 and the ground to be 0.1. Your program should report that the assembly must begin to collapse.
- Assembly that can continue to stand. Next, test your program with the following values: the mass of body 1 is 2, the mass of body 2 is 10, and the friction coefficient at all four contacts is 0.5. Your program should report that there is a set of contact forces that results in equilibrium (the assembly remaining standing).
What to Submit
You will submit a single .zip file with the following contents:
1. Your commented code in a directory called "code." Your code should be lightly commented, so it is clear to the reader what the code is doing. No need to go overboard, but keep in mind your reviewer may not be fluent in your programming language. Your code comments must include an example of how to use the code. You can write your program in any language, provided it is clearly structured, reasonably modular, easy to understand for a reader with no experience in your programming language, and with sufficient comments. Your program can span multiple files, or it can be a single file, if appropriate. If your code is in Mathematica, turn in (a) your .nb notebook file and (b) a .pdf printout of your code, so a reviewer can read your code without having to have the Mathematica software.
2. A directory called "results." In this directory you should have
- An output log showing your program being called and the resulting output for the case of the collapsing assembly and the assembly that can continue to stand described in the section "Testing Your Program" above. The figure on this page shows the assembly and the text above gives the body masses and friction coefficients for these two cases.
- A drawing of another assembly of your own design. This assembly should have at least two bodies in addition to ground. This drawing should clearly indicate the center of mass and contact locations, as well as the masses of each body. You could use the three-body arch in Figure 12.27 as your assembly if you'd like (choose your own contact and center of mass locations that agree approximately with the figure). Without changing the masses of the bodies, this assembly must begin to collapse for one set of friction coefficients at the contacts and should be able to stand for another set of friction coefficients.
- An output log showing your program being called with your assembly from the previous bullet, for a choice of friction coefficients where the assembly must begin to collapse and another set of choices where it can continue to stand. For each of the two cases, you should provide a brief explanation of the results. For example, for the case where the assembly can continue to stand, you can use your linear programming solution for to draw the contact wrenches for each body, graphically showing that the sum of the contact wrenches cancels the gravity wrench.
3. (OPTIONAL). For the three-body arch in Figure 12.27 in the book, assume all three bodies are identical, with the same masses and friction coefficients. Use your program to determine the minimum friction coefficient that keeps the assembly standing.
4. (OPTIONAL) A plain text file called "README.txt" or other explanatory file. This has any other information that may help the reviewer understand your submission.









